设{an}为等差数列,{bn}为等比数列,a1=b1=1,a2+a4=b3,b2b4=a3,分别求出{an}及{bn}的前10项的和S10及T10
解:∵{a
n}为等差数列,{b
n}为等比数列,
∴a
2+a
4=2a
3,b
2b
4=b
32已知a
2+a
4=b
3,b
2b
4=a
3,
∴b
3=2a
3,a
3=b
32得b
3=2b
32∵b
3≠0∴

由a
1=1,
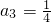
知{a
n}的公差为
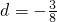
,
∴
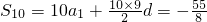
,
由b
1=1,
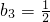
知{b
n}的公比为
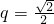
或

.
当
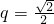
时,
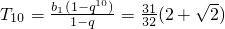
,
当

时,

.
分析:根据等差数列的性质可知a
2+a
4=2a
3,根据等比数列的性质可知b
2b
4=b
32,而已知a
2+a
4=b
3,b
2b
4=a
3,所以得到b
3=2a
3,a
3=b
32,两者联立,由b
3≠0,即可求出a
3与b
3的值,然后分别根据a
1=b
1=1,利用等差及等比数列的通项公式求出等差数列的公差d及等比数列的公比q,然后根据等差、等比数列的前n项和的公式即可求出{a
n}及{b
n}的前10项的和S
10及T
10的值.
点评:此题考查学生灵活运用等差、等比数列的通项公式及等差、等比数列的前n项和的公式化简求值,是一道综合题.


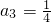 知{an}的公差为
知{an}的公差为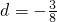 ,
,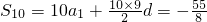 ,
,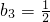 知{bn}的公比为
知{bn}的公比为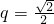 或
或 .
.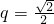 时,
时,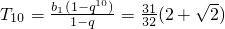 ,
, 时,
时, .
.
