
| 2 |
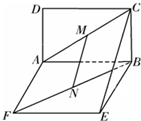
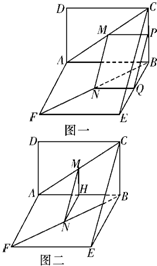
| AM |
| AC |
| AH |
| AB |
| FN |
| FB |
| AH |
| AB |
| 2 |
| AM |
| AC |
| FN |
| FB |
| AH |
| AB |
| MH |
| BC |
| 1 |
| 3 |
| 5 |


科目:高中数学 来源: 题型:
 如图,将边长为3的正方形ABCD绕中心O顺时针旋转α (0<α<
如图,将边长为3的正方形ABCD绕中心O顺时针旋转α (0<α<| π |
| 2 |
| π |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
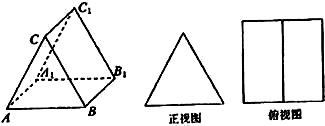 如图,三棱柱的侧棱长和底面边长均为2,且侧棱AA1⊥平面A1B1C1,它的正视图是等边三角形,俯视图是由两个全等的矩形组成的正方形,该三棱柱的侧视图面积为( )
如图,三棱柱的侧棱长和底面边长均为2,且侧棱AA1⊥平面A1B1C1,它的正视图是等边三角形,俯视图是由两个全等的矩形组成的正方形,该三棱柱的侧视图面积为( )| A、4 | ||
B、2
| ||
C、2
| ||
D、
|
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2012•浦东新区一模)如图所示,在平面直角坐标系xOy上放置一个边长为1的正方形PABC,此正方形PABC沿x轴滚动(向左或向右均可),滚动开始时,点P位于原点处,设顶点P(x,y)的纵坐标与横坐标的函数关系是y=f(x),x∈R,该函数相邻两个零点之间的距离为m.
(2012•浦东新区一模)如图所示,在平面直角坐标系xOy上放置一个边长为1的正方形PABC,此正方形PABC沿x轴滚动(向左或向右均可),滚动开始时,点P位于原点处,设顶点P(x,y)的纵坐标与横坐标的函数关系是y=f(x),x∈R,该函数相邻两个零点之间的距离为m.| 函数性质 | 结 论 | |
| 奇偶性 | 偶函数 偶函数 | |
| 单调性 | 递增区间 | [4k,4k+2],k∈z [4k,4k+2],k∈z |
| 递减区间 | [4k-2,4k],k∈z [4k-2,4k],k∈z | |
| 零点 | x=4k,k∈z x=4k,k∈z | |
查看答案和解析>>
科目:高中数学 来源:2012年上海市浦东新区高考数学一模试卷(理科)(解析版) 题型:解答题
| 函数性质 | 结 论 | |
| 奇偶性 | ______ | |
| 单调性 | 递增区间 | ______ |
| 递减区间 | ______ | |
| 零点 | ______ | |

查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,将边长为3的正方形ABCD绕中心O顺时针旋转α (0<α<
如图,将边长为3的正方形ABCD绕中心O顺时针旋转α (0<α< )得到正方形A′B′C′D′.根据平面几何知识,有以下两个结论:
)得到正方形A′B′C′D′.根据平面几何知识,有以下两个结论: ),△EAL,△EA′F,△GBF,△GB′H,△ICH,△IC′J,△KDJ,△KD′L均是全等三角形.
),△EAL,△EA′F,△GBF,△GB′H,△ICH,△IC′J,△KDJ,△KD′L均是全等三角形.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com