
对于函数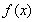 ,若存在区间
,若存在区间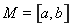 ,使得
,使得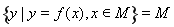 ,则称区间
,则称区间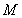 为函数
为函数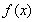 的一个“好区间”.给出下列4个函数:
的一个“好区间”.给出下列4个函数:
①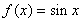 ;②
;②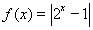 ;③
;③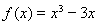 ;④
;④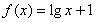 .
.
其中存在“好区间”的函数是 .(填入所有满足条件函数的序号)
②③④
【解析】
试题分析:①函数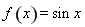 在
在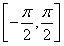 上是单调增函数,若函数在
上是单调增函数,若函数在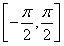 上存“好区间”
上存“好区间”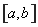 则必有
则必有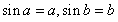 ,即方程
,即方程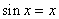 有两个根,令
有两个根,令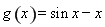
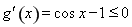
在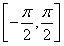 上恒成立,所以函数
上恒成立,所以函数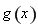 在
在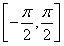 上为减函数,则函数
上为减函数,则函数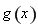 在
在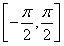 上至多一个零点,即方程
上至多一个零点,即方程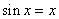 在
在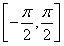 上不可能有两个解,又因为函数
上不可能有两个解,又因为函数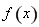 的值域为
的值域为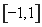 ,所以当
,所以当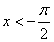 或
或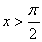 时,方程
时,方程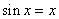 无解.所以函数
无解.所以函数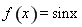 没有“好区间”;
没有“好区间”;
②对于函数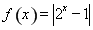 ,该函数在
,该函数在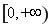 上是增函数由幂函数的性质我们易得,
上是增函数由幂函数的性质我们易得,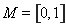 时,
时,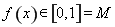 ,所以
,所以 为函数
为函数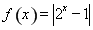 的一个“好区间”.
的一个“好区间”.
③对于函数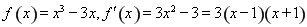 当
当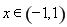 时
时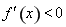 ,所以函数
,所以函数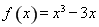 的增区间有
的增区间有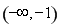 和
和 ,减区间是
,减区间是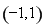 ,取
,取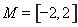 ,此时
,此时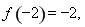
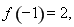
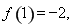
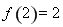 ,所以函数
,所以函数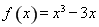 在
在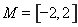 上的值域了是
上的值域了是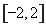 ,则
,则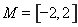 为函数的一个“好区间”;
为函数的一个“好区间”;
④函数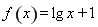 在定义域
在定义域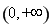 上为增函数,若有“好区间”
上为增函数,若有“好区间”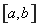
 则
则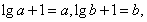 也就是函数
也就是函数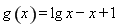 有两个零点,显然
有两个零点,显然 是函数的一个零点,由
是函数的一个零点,由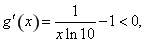
得,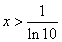 ,函数
,函数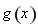 在
在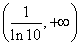 上为减函数;由
上为减函数;由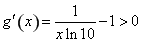 ,得
,得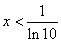 ,函数在
,函数在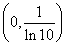 上为增函数.所以
上为增函数.所以 的最大值为
的最大值为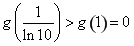 ,则该函数
,则该函数  在
在
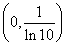 上还有一个零点.所以函数
上还有一个零点.所以函数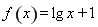 存在“好区间”.
存在“好区间”.
考点:1、函数的单调性;2、函数的零点3、函数的定义域和值域.


科目:高中数学 来源:2013-2014学年浙江省高三上学期期中考试文科数学试卷(解析版) 题型:填空题
对于函数 ,若存在区间
,若存在区间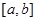 ,当
,当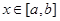 时,函数
时,函数 的值域为
的值域为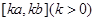 ,则称
,则称 为
为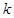 倍值函数. 若
倍值函数. 若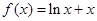 是
是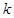 倍值函数,则实数
倍值函数,则实数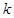 的取值范围是___________.
的取值范围是___________.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年福建省四地六高三第三次月考理科数学试卷(解析版) 题型:填空题
对于函数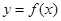 ,若存在区间
,若存在区间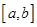 ,当
,当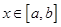 时的值域为
时的值域为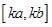
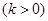 ,则称
,则称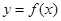 为
为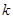 倍值函数.若
倍值函数.若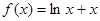 是
是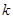 倍值函数,则实数
倍值函数,则实数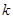 的取值范围是 。
的取值范围是 。
查看答案和解析>>
科目:高中数学 来源:2011-2012学年山东省高三第二次月考文科数学试卷 题型:选择题
对于函数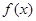 ,若存在区间
,若存在区间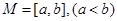 ,使得
,使得 ,则称区间
,则称区间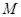 为函数
为函数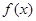 的一个“稳定区间”.现有四个函数:
的一个“稳定区间”.现有四个函数:
①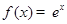 ; ②
; ②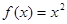 ③
③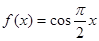 ④
④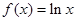 .其中存在“稳定区间”的函数的个数为(
)
.其中存在“稳定区间”的函数的个数为(
)
A.1 B.2 C.3 D.4
查看答案和解析>>
科目:高中数学 来源:2012届福建省高三上学期11月考文科试卷 题型:选择题
对于函数 ,若存在区间
,若存在区间 ,使得
,使得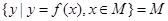 ,则称区间
,则称区间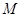 为函数
为函数 的一个“稳定区间”.现有四个函数:
的一个“稳定区间”.现有四个函数:
①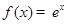 ; ②
; ②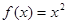 ③
③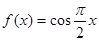 ④
④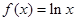 .其中存在“稳定区间”的函数的个数为
.其中存在“稳定区间”的函数的个数为
A.1 B.2 C.3 D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com