
20.(甲)如图,以正四棱锥V-ABCD底面中心O为坐标原点建立空间直角坐标系O-xyz,其中Ox∥BC,
Oy∥AB.E为VC中点,正四棱锥底面边长为2a,高为h.
(Ⅰ)求cos<![]() >;
>;
(Ⅱ)记面BCV为![]() ,面DCV为
,面DCV为![]() ,若∠BED是二面角
,若∠BED是二面角![]() -VC-
-VC-![]() 的平面角,求∠BED.
的平面角,求∠BED.
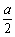
20.(甲)本小题主要考查空间直角坐标的概念,空间点和向量的坐标表示以及两个向量夹角的计算方法;考查运用向量研究空间图形的数学思想方法.
解:(Ⅰ)由题意知B(a,a,0),C(-a,a,0),D(-a,-a,0),E(-![]() ,
,![]() ,
,![]() ).
).
由此得 ![]() =(-
=(-![]() ,-
,-![]() ,
,![]() ),
),![]() =(
=(![]() ,
,![]() ,
,![]() ).
).
∴![]() ·
·![]() =(-
=(-![]() ·
·![]() )+(-
)+(-![]() ·
·![]() )+
)+![]() ·
·![]() =-
=-![]() +
+![]() .
.
|![]() |=|
|=|![]() |=
|=![]() =
=![]() .
.
由向量的数量积公式有
cos<![]() ,
,![]() >=
>=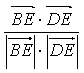
=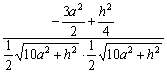
=![]() .
.
(Ⅱ)若∠BED是二面角![]() -VC-
-VC-![]() 的平面角,则
的平面角,则![]() ⊥
⊥![]() ,即有
,即有![]() ·
·![]() =0.
=0.
又由C(-a,a,0),V(0,0,h), 有![]() =(a,-a,h),且
=(a,-a,h),且![]() =(-
=(-![]() ,-
,-![]() ,
,![]() ),
),
∴![]() ·
·![]() =-
=-![]() +
+![]() +
+![]() =0.
=0.
即h=![]() ,这时有 cos<
,这时有 cos<![]() ,
,![]() >=
>=![]() =
=![]() =-
=-![]() .
.
∴∠BED=<![]() ,
,![]() >=arccos(-
>=arccos(-![]() )=
)=![]() -arccos
-arccos![]() .
.


 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:高中数学 来源: 题型:
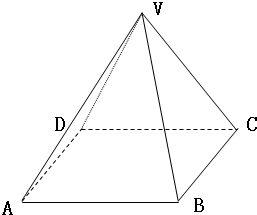 如图,以正四棱锥V-ABCD底面中心O为坐标原点建立空间直角坐标系O-xyz,其中Ox∥BC,Oy∥AB;已知VA=kAB,点E是VC的中点,底面正方形ABCD边长为2a,高为h.
如图,以正四棱锥V-ABCD底面中心O为坐标原点建立空间直角坐标系O-xyz,其中Ox∥BC,Oy∥AB;已知VA=kAB,点E是VC的中点,底面正方形ABCD边长为2a,高为h.| BE |
| DE |
查看答案和解析>>
科目:高中数学 来源: 题型:
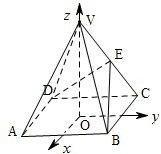 (2001•江西)如图,以正四棱锥V-ABCD底面中心O为坐标原点建立空间直角坐标系O-xyz,其中Ox∥BC,Oy∥AB.E为VC中点,正四棱锥底面边长为2a,高为h.
(2001•江西)如图,以正四棱锥V-ABCD底面中心O为坐标原点建立空间直角坐标系O-xyz,其中Ox∥BC,Oy∥AB.E为VC中点,正四棱锥底面边长为2a,高为h.| BE |
| DE |
查看答案和解析>>
科目:高中数学 来源: 题型:
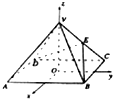 (2001•江西)如图,以正四棱锥V-ABCD底面中心O为坐标原点建立空间直角坐标系O-xyz,其中Ox∥BC,Oy∥AB.E为VC中点,正四棱锥底面边长为2a,高为h.
(2001•江西)如图,以正四棱锥V-ABCD底面中心O为坐标原点建立空间直角坐标系O-xyz,其中Ox∥BC,Oy∥AB.E为VC中点,正四棱锥底面边长为2a,高为h.| BE |
| DE |
查看答案和解析>>
科目:高中数学 来源: 题型:
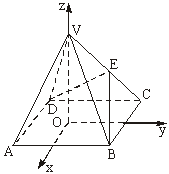
20.(甲)如图,以正四棱锥V-ABCD底面中心O为坐标原点建立空间直角坐标系O-xyz,其中Ox∥BC,
Oy∥AB.E为VC中点,正四棱锥底面边长为2a,高为h.
(Ⅰ)求cos〈![]() 〉;
〉;
(Ⅱ)记面BCV为![]() ,面DCV为
,面DCV为![]() ,若∠BED是二面角
,若∠BED是二面角![]() -VC-
-VC-![]() 的平面角,求cosBED的值.
的平面角,求cosBED的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com