
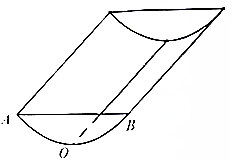
 某小区内有一条形状如图的沟渠,沟沿是两条平行线段,沟渠宽AB为20厘米,沟渠的直截面ABO为一段抛物线,抛物线顶点为O,对称轴与地面垂直,沟渠深20厘米,沟渠中水深10厘米.
某小区内有一条形状如图的沟渠,沟沿是两条平行线段,沟渠宽AB为20厘米,沟渠的直截面ABO为一段抛物线,抛物线顶点为O,对称轴与地面垂直,沟渠深20厘米,沟渠中水深10厘米.分析 (1)如图所示,以O为坐标原点,建立直角坐标系.设抛物线方程为:y=ax2(a>0).把(10,20)代入解得a,把y=10代入抛物线方程可得x.
(2)为使所挖土最少,等腰梯形的两腰必须与抛物线相切,设切点为P$(t,\frac{1}{5}{t}^{2})$(0<t≤10)是抛物线OB上的一点,设经过点P的切线CD的方程为:y-$\frac{1}{5}{t}^{2}$=k(x-t),与抛物线方程联立可得:x2-5kx+5kt-t2=0,由△=0,解得k=$\frac{2}{5}$t,kd 切线方程为:$y=\frac{2}{5}tx-\frac{1}{5}{t}^{2}$,可得C$(\frac{t}{2},0)$,D$(\frac{t}{2}+\frac{50}{t},20)$.kd 梯形OCDE的面积S=10(t+$\frac{50}{t}$),即可得出.
解答 解:(1)如图所示,以O为坐标原点,建立直角坐标系.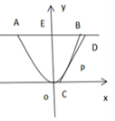
设抛物线方程为:y=ax2(a>0).
把(10,20)代入可得:20=a×102,解得a=$\frac{1}{5}$,可得$y=\frac{1}{5}{x}^{2}$.
把y=10代入可得x2=50,x=$±5\sqrt{2}$,
∴水面宽为10$\sqrt{2}$厘米.
(2)为使所挖土最少,等腰梯形的两腰必须与抛物线相切,设切点为P$(t,\frac{1}{5}{t}^{2})$(0<t≤10)是抛物线OB上的一点,设经过点P的切线CD的方程为:y-$\frac{1}{5}{t}^{2}$=k(x-t),与抛物线方程联立可得:
x2-5kx+5kt-t2=0,由△=0,解得k=$\frac{2}{5}$t,
∴切线方程为:$y=\frac{2}{5}tx-\frac{1}{5}{t}^{2}$,可得C$(\frac{t}{2},0)$,D$(\frac{t}{2}+\frac{50}{t},20)$.梯形OCDE的面积S=10(t+$\frac{50}{t}$)≥10×$2\sqrt{t•\frac{50}{t}}$=100$\sqrt{2}$,当且仅当t=5$\sqrt{2}$时取等号.此时OC=$\frac{5\sqrt{2}}{2}$.
即沟渠底部宽为5$\sqrt{2}$厘米时,所挖土最少.
点评 本题考查了抛物线的标准方程及其性质、切线方程、等腰梯形的面积计算公式,考查了推理能力与计算能力,属于中档题.


 单元期中期末卷系列答案
单元期中期末卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
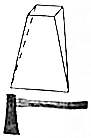 斧头的形状叫楔形,在《算数书》中又称之为“郓(y$\stackrel{、}{u}$n)都”或“壍(qi$\stackrel{、}{a}$n)堵”:其上底是一矩形,下底是一线段.有一斧头:上厚为三,下厚为六,高为五及袤(m$\stackrel{、}{a}$o)为二,问此斧头的体积为几何?意思就是说有一斧头形的几何体,上底为矩形,下底为一线段,上底的长为3,下底线段长为6,上下底间的距离(高)为5,上底矩形的宽为2,则此几何体的体积是( )
斧头的形状叫楔形,在《算数书》中又称之为“郓(y$\stackrel{、}{u}$n)都”或“壍(qi$\stackrel{、}{a}$n)堵”:其上底是一矩形,下底是一线段.有一斧头:上厚为三,下厚为六,高为五及袤(m$\stackrel{、}{a}$o)为二,问此斧头的体积为几何?意思就是说有一斧头形的几何体,上底为矩形,下底为一线段,上底的长为3,下底线段长为6,上下底间的距离(高)为5,上底矩形的宽为2,则此几何体的体积是( )| A. | 6 | B. | 10 | C. | 16 | D. | 20 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com