Question

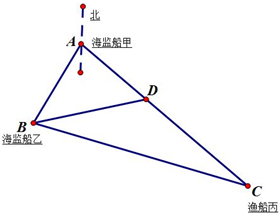
如图，正在中国钓鱼岛附近的A处执行任务的海监船甲和在B处执行任务的海监船乙，同时收到同一片海域上一艘渔船丙的求救信号，此时渔船丙在海监船甲的南偏东40°方向距海监船甲70km的C处，海监船乙在海监船甲的南偏西20°方向的B处，两艘海监船协调后立即让海监船甲向渔船丙所在的位置C处沿直线AC航行前去救援，海监船乙仍留在B处执行任务，海监船甲航行30km到达D处时，收到新的指令另有重要任务必须执行，于是立即通知在B处执行任务的海监船乙前去救援渔船丙（海监船乙沿直线BC航行前去救援渔船丙），此时B、D两处相距42km，问海监船乙要航行多少距离才能到达渔船丙所在的位置C处实施营救．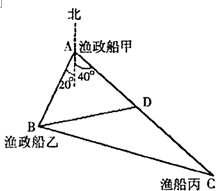

Answer 1

分析：设∠ABD=α，在△ABD中，利用正弦定理求出sinα或α的大小，再在△BDC中，利用余弦定理求解即可．

解答：解：


设∠ABD=α，在△ABD中，AD=30，BD=42，∠BAD=60°，由正弦定理得：

AD

sinα

=

BD

sin∠BAD

，sinα=

AD

BD

sin∠BAD=

30

42

sin60°=

5 3

14

，
又∵AD＜BD
∴0°＜α＜60°，
cosα=

1-sin2α

=

11

14

cos∠BDC=cos(60°+α)=-

1

7

，
在△BDC中，由余弦定理得：BC²=DC²+BD²-2DC•BDcos∠BDC=40²+42²-80×42cos（60°+α）=3844
∴BC=62（km）
答：渔政船乙要航行62km才能到达渔船丙所在的位置C处实施营救

点评：本题考查正弦定理、余弦定理在实际问题中的应用．要将实际问题中的数据转化为三角形中的数据，根据条件选择合适定理直接求解或借用方程间接求解．