A
分析:有x,y满足条件:
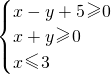
可以画出可行域,令z=(x+1)
2+y
2 此式子可以可能成以(-1,0)为圆心,半径随z的变化而变化的圆系方程,利用此目标函数的几何含义可求出.
解答:有x,y满足条件:
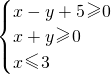
可以画出可行域为图示的阴影图形:
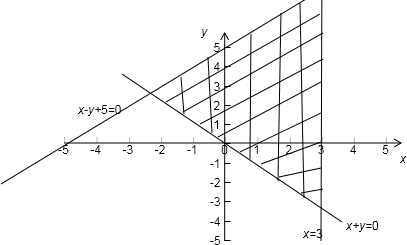
对于目标函数令z=(x+1)
2+y
2 此式子可以可能成以(-1,0)为圆心,半径随z的变化而变化的圆系方程,当目标函数过
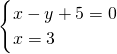
?(3,8)时,使得目标函数z取得最大,最大值为:z=80.
故选A
点评:此题考查了有线性约束条件画出可行域,利用目标函数的几何含义求函数的最值,重点考查了学生的数形结合的思想.

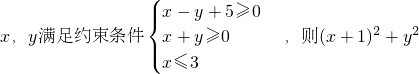 的最大值为
的最大值为
