设数列an的前n项和为Sn,对n∈N*,都有an=5Sn+2成立,
(Ⅰ) 求数列an的通项公式;
(Ⅱ)设数列bn=log2|an|,试求数列bn的前n项和Mn.
解:(Ⅰ)当n=1时,a
1=5S
1+2=5a
1+2,
∴

,
当n≥2时,a
n=S
n-S
n-1=
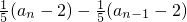
,
∴

,即
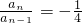
,
∴数列{a
n}成等比数列,其首项

,公比为

,
∴数列a
n的通项公式
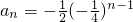
;
(Ⅱ)由(Ⅰ)知a
n=(-1)
n•2
1-2n,
∴b
n=log
2|a
n|=1-2n,
∵b
n+1-b
n=-2,
∴{a
n}为等差数列,且首相为b
1=-1,公差为-2,
∴
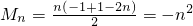
.
分析:(Ⅰ)把n=1代入a
n=5S
n+2,即可求出首项的值,当n大于等于1时,利用a
n=S
n-S
n-1,即可确定出此数列为等比数列,且得到等比数列的公比的值,根据求出的首项和公比写出通项公式即可;
(Ⅱ)把(Ⅰ)中求出的通项公式代入b
n=log
2|a
n|中,利用对数的运算法则化简后,即可确定出数列{b
n}为等差数列,分别求出等差数列的首项和公差,根据等差数列的前n项和公式求出数列{b
n}的前n项和M
n即可.
点评:此题考查学生掌握等比数列及等差数列的确定方法,灵活运用等比数列的通项公式及等差数列的前n项和的公式化简求值,是一道中档题.

 ,
,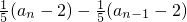 ,
, ,即
,即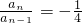 ,
, ,公比为
,公比为 ,
,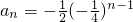 ;
;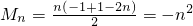 .
.
