设A,B两城相距100km,在两城市之间距A城xkm处的D处建一个发电厂给A,B两城市供电.为了城市环保,发电厂与城市的距离不得小于40km,已知供电费用(元)与供电距离(km)的平方和供电量(亿度)之积成正比,比例系数λ=0.9.若A城的供电量为20亿度/月,B城供电量为10亿度/月.
(1)将月供电总费用y(元)表示成x(km)的函数,并求其定义域;
(2)发电厂建在距A城多远处,才能使供电费用最少?并求出供电费用的最小值.
解:(1)∵发电厂与城市的距离不得小于40km,又∵A,B两城相距100km,
∴x的取值范围为40≤x≤60;
∵供电费用(元)与供电距离(km)的平方和供电量(亿度)之积成正比,比例系数λ=0.9,
又∵A城的供电量为20亿度/月,B城供电量为10亿度/月
∴y=0.9×20×x
2+0.9×10×(100-x)
2化简得:y=27x
2-1800x+90000(40≤x≤60);
(2)由y=27x
2-1800x+90000=27
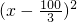
+60000.
因为对称轴x=

不在定义域内
则二次函数在[40,60]上单调递增
所以当x=40米时,y最小.
答:故当发电站建在距A城40千米时,才能使供电总费用最小,最小值为61200元.
分析:(1)由已知中发电厂与城市的距离不得小于40km,A、B两座城市相距100km,我们易求出求x的范围,由已知中供电费用与“供电距离的平方与供电量之积”成正比,比例系数k=0.9,若A城市供电量为20亿度/月,B城市为10亿度/月,结合x的取值范围,即可得到月供电总费用y表示成x的函数;
(2)由(1)所得的函数解析式,结合二次函数性质,先进行配方,开口向上,对称轴为

不在定义域内,根据函数的单调性可知当x=40米时,y最小.
点评:本题考查的知识点是根据实际问题选择函数类型,二次函数的性质,其中在利用函数数学模型解答实际问题时,定义域(自变量x的取值范围)是易忽略而致错的点.

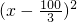 +60000.
+60000. 不在定义域内
不在定义域内 不在定义域内,根据函数的单调性可知当x=40米时,y最小.
不在定义域内,根据函数的单调性可知当x=40米时,y最小.
