
分析 (1)求f(-x)=-f(x),从而说明f(x)为R上的奇函数;
(2)根据增函数的定义,设任意的x1,x2∈R,且x1<x2,然后作差,通分,提取公因式,证明f(x1)<f(x2),便可得出f(x)在R上单调递增;
(3)根据f(x)为奇函数且在R为增函数,便可由f(x-k)+f(x2-k2)≥0恒成立得到x-k≥k2-x2恒成立,即x2+x-k2-k≥0恒成立,从而有△≤0,这样即可得出k的值.
解答 解:(1)$f(-x)=\frac{{e}^{-x}-{e}^{x}}{2}=-f(x)$;
∴f(x)为奇函数;
(2)证明:设x1<x2,则:$f({x}_{1})-f({x}_{2})=\frac{{e}^{{x}_{1}}-{e}^{-{x}_{1}}}{2}-\frac{{e}^{{x}_{2}}-{e}^{-{x}_{2}}}{2}$=$\frac{({e}^{{x}_{1}}-{e}^{{x}_{2}})(1+\frac{1}{{e}^{{x}_{1}+{x}_{2}}})}{2}$;
∵x1<x2;
∴${e}^{{x}_{1}}<{e}^{{x}_{2}}$,${e}^{{x}_{1}}-{e}^{{x}_{2}}<0$;
∴f(x1)<f(x2);
∴f(x)在R上是增函数;
(3)∵f(x)为奇函数,且在R上为增函数;
∴由f(x-k)+f(x2-k2)≥0得,f(x-k)≥f(k2-x2);
∴x-k≥k2-x2;
∴x2+x-k2-k≥0在R上恒成立;
∴△=1+4(k2+k)≤0;
∴(2k+1)2≤0;
∴2k+1=0;
∴$k=-\frac{1}{2}$;
即存在实数k=$-\frac{1}{2}$,使f(x-k)+f(x2-k2)≥0恒成立.
点评 考查奇函数的定义,增函数的定义,以及根据增函数定义证明一个函数为增函数的方法和过程,作差的方法比较f(x1)与f(x2),作差后为分式的一般要通分,一般要提取公因式,指数函数的单调性,一元二次不等式恒成立时判别式△的取值情况.


科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | π | C. | π2 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
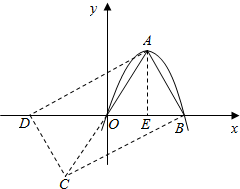 如果一条抛物线y=ax2+bx+c(a≠0)与x轴有两个交点,那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”.
如果一条抛物线y=ax2+bx+c(a≠0)与x轴有两个交点,那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{ab}m$ | B. | $\frac{a+b}{2}m$ | C. | am | D. | bm |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 120° | B. | 30° | C. | 150° | D. | 60° |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com