
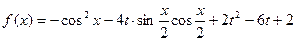 (
(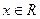 ).
).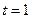 时,求
时,求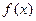 的最小值;
的最小值;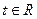 ,将
,将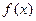 的最小值记为
的最小值记为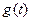 ,求
,求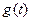 的表达式;
的表达式;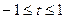 时,关于
时,关于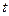 的方程
的方程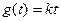 有且仅有一个实根,求实数
有且仅有一个实根,求实数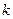 的取值范围.
的取值范围.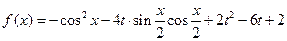
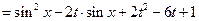
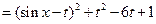 ,……………………………2分
,……………………………2分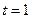
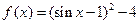
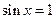 时,
时,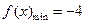 ………………………………………………4分
………………………………………………4分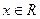 ,∴
,∴ 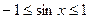 ,
,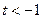 时,则
时,则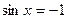 时,
时,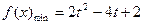 ;
;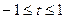 时,则
时,则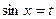 时,
时,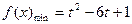 ;
;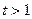 时,则当
时,则当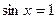 时,
时,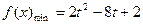 ;
;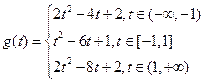 . ……………………………8分
. ……………………………8分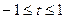 时,
时,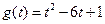 ,
,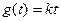 即
即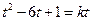 ,
, 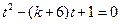 在区间
在区间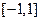 有且仅有一个实根,……………………………9分
有且仅有一个实根,……………………………9分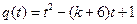 ,则有:
,则有: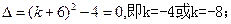
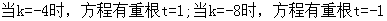
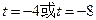 ………………………………………………………………10分
………………………………………………………………10分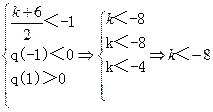 或
或 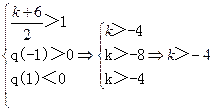
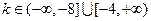 时,方程
时,方程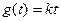 在区间
在区间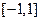 有且仅有一个实根.……14分
有且仅有一个实根.……14分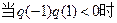 ,
, 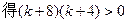 ,
,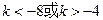 ; …………………………………………………………………10分
; …………………………………………………………………10分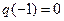 时,
时,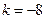 ,此时
,此时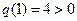 ,符合题意;
,符合题意;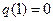 时,
时, 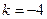 ,此时
,此时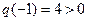 ,符合题意;
,符合题意;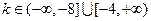 时,方程
时,方程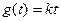 在区间
在区间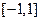 有且仅有一个实根.……14分
有且仅有一个实根.……14分

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:不详 题型:解答题
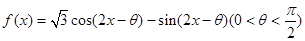 是偶函数.
是偶函数.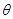 ;
;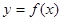 的图像先纵坐标不变,横坐标缩短为原来的
的图像先纵坐标不变,横坐标缩短为原来的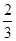 倍,再向左平移
倍,再向左平移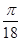 个单位,然后向上平移1个单位得到
个单位,然后向上平移1个单位得到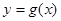 的图像,若关于
的图像,若关于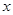 的方程
的方程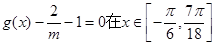 有且只有两个不同的根,求
有且只有两个不同的根,求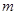 的范围.
的范围.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
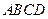 ,
,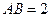 ,
,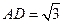 ,
,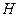 是
是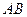 的中点,在该花园中有一花圃其形状是以
的中点,在该花园中有一花圃其形状是以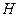 为直角顶点的内接Rt△
为直角顶点的内接Rt△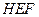 ,其中E、F分别落在线段
,其中E、F分别落在线段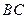 和线段
和线段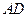 上如图.分别记
上如图.分别记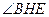 为
为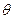 (
(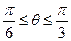 ),
),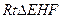 的周长为
的周长为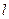 ,
,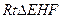 的面积为
的面积为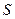 。
。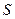 的取值范围;
的取值范围;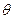 为何值时
为何值时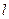 的值为最小;并求
的值为最小;并求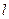 的最小值
的最小值
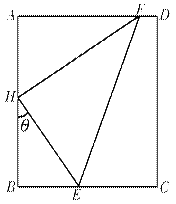
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com