
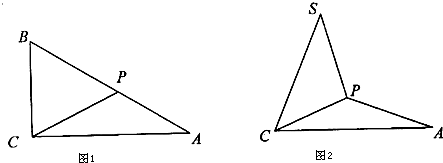
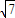 (图2).
(图2).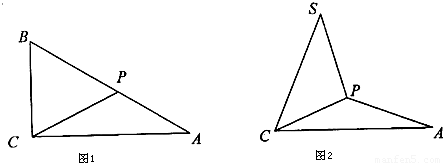
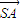 ,利用SA=
,利用SA= ,即可求得∠SCP的度数;
,即可求得∠SCP的度数;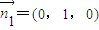 ,平面ASC的法向量为
,平面ASC的法向量为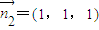 ,利用向量的夹角公式,即可求得二面角P-SC-A的余弦值.
,利用向量的夹角公式,即可求得二面角P-SC-A的余弦值.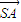 =(2cosα-3sinα,3cosα,-2sinα),
=(2cosα-3sinα,3cosα,-2sinα),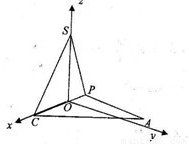
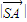 =
=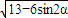 =
=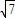 ,∴sin2α=1,∴α=
,∴sin2α=1,∴α=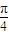
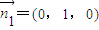
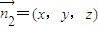
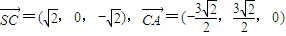
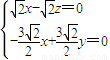 ,∴取
,∴取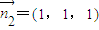
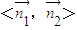 =
= =
=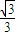
 .
.

科目:高中数学 来源: 题型:
| 7 |
查看答案和解析>>
科目:高中数学 来源: 题型:
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源:2012-2013学年吉林省白山市长白山一高高一(上)综合检测数学试卷(解析版) 题型:填空题
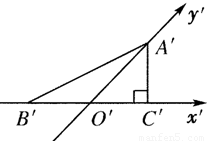
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com