
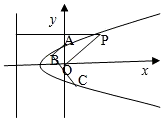
 已知向量n=(1,0),点A(0,2),动点P满足:|
已知向量n=(1,0),点A(0,2),动点P满足:|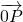 |比向量
|比向量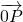 在n的方向上的投影多2.
在n的方向上的投影多2.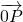 在n的方向上的投影为|
在n的方向上的投影为|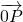 |cos∠POx,即P点到y轴的距离,又|
|cos∠POx,即P点到y轴的距离,又|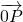 |比向量
|比向量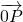 在n的方向上的投影多2,
在n的方向上的投影多2, y12-1,y1),C(
y12-1,y1),C( y22-1,y2),
y22-1,y2), =(
=( y12-1,y1-2)=
y12-1,y1-2)= ( y1-2)(y1+2,4),
( y1-2)(y1+2,4), =(
=( y22-
y22- y12,y2-y1)=
y12,y2-y1)= ( y2-y1) (y2+y1,4),
( y2-y1) (y2+y1,4), •
• =0,即
=0,即 ( y1-2)
( y1-2) ( y2-y1)[(y1+2)(y2+y1)+16]=0,
( y2-y1)[(y1+2)(y2+y1)+16]=0,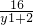 -y1=2-(
-y1=2-(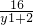 +y1+2).由均值不等式得y2≥10或y2≤-6.
+y1+2).由均值不等式得y2≥10或y2≤-6.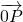 在n的方向上的投影为|
在n的方向上的投影为|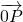 |cos∠POx,即P点到y轴的距离,又|
|cos∠POx,即P点到y轴的距离,又|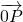 |比向量
|比向量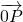 在n的方向上的投影多2,得出P点到原点的距离等于它到直线x=-2的距离,最后根据抛物线的定义得出所求的轨迹方程;
在n的方向上的投影多2,得出P点到原点的距离等于它到直线x=-2的距离,最后根据抛物线的定义得出所求的轨迹方程;

科目:高中数学 来源: 题型:
 已知向量n=(1,0),点A(0,2),动点P满足:|
已知向量n=(1,0),点A(0,2),动点P满足:|| 0P |
| 0P |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
A.
| B.
| C.
| D.
|
查看答案和解析>>
科目:高中数学 来源:2009年湖北省武汉市硚口区高三数学交流试卷1(文理合卷)(解析版) 题型:解答题
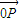 |比向量
|比向量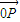 在n的方向上的投影多2.
在n的方向上的投影多2.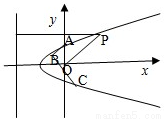
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com