Question

（1）用1、2、3、4、5、6、7可组成多少个无重复数字的四位数且四位数为偶数；

（2）用0、1、2、3、4、5可组成多少无重复数字的且可被5整除的五位数. (用数字作答)

 

Answer 1

【答案】

（1）360（2）216

【解析】

试题分析：解：（1）根据题意，由于用1、2、3、4、5、6、7可组成多少个无重复数字的四位数，且是偶数，那么末尾是偶数，有3种，其余的任意选择三个，即从剩下的6个总选3个排列即可，得到为,根据分步乘法计数原理可知为360    

（2）根据题意，由于用0、1、2、3、4、5可组成多少无重复数字的且可被5整除的五位数，那么额控制末尾数为0，或者5，需要分情况有零的情况和无零的情况，没有零，则总剩下的四个数字中任意选4个即可，有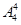=24，而有零，则0不在首尾，末尾是5，和末尾是0，则所有的情况为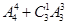,分布加法原理得到共有216     

考点：分步计数原理

点评：本题考查分步计数原理，是一个数字问题，数字问题是排列中的一大类问题，把排列问题包含在数字问题中，解题的关键是看清题目的实质，很多题目要分类讨论，要做到不重不漏