
【题目】如图,直三棱柱ABC﹣A1B1C1中,CA=CB,M,N,P分别为AB,A1C1 , BC的中点. 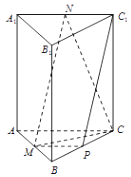
求证:
(1)C1P∥平面MNC;
(2)平面MNC⊥平面ABB1A1 .
【答案】
(1)证明:连接MP,因为M、P分别为AB,BC的中点
∵MP∥AC,MP= ![]() ,
,
又因为在直三棱柱ABC﹣A1B1C1中,∴AC∥A1C1,AC=A1C1
且N是A1C1的中点,∴MP∥C1N,MP=C1N
∴四边形MPC1N是平行四边形,∴C1P∥MN
∵C1P面MNC,MN面MNC,∴C1P∥平面MNC;
(2)证明:在△ABC中,CA=CB,M为AB的中点,∴CM⊥AB.
在直三棱柱ABC﹣A1B1C1中,B1B⊥面ABC.
∵CM面ABC,∴BB1⊥CM
由因为BB1∩AB=B,BB1,AB平面面ABB1A1
又CM平面MNC,
∴平面MNC⊥平面ABB1A1.
【解析】(1)连接MP,只需证明四边形MPC1N是平行四边形,即可得MN∥C1P∵C1P,即可证得C1P∥平面MNC;(2)只需证明CM⊥平面MNC,即可得平面MNC⊥平面ABB1A1.


科目:高中数学 来源: 题型:
【题目】某市电视台为了宣传,举办问答活动,随机对该市15至65岁的人群进行抽样,频率分布直方图及回答问题统计结果如表所示:
组号 | 分组 | 回答正确 | 回答正确的人数 |
第1组 | [15,25) | 5 | 0.5 |
第2组 | [25,35) | a | 0.9 |
第3组 | [35,45) | 27 | x |
第4组 | [45,55) | b | 0.36 |
第5组 | [55,65) | 3 | y |
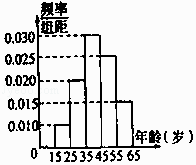
(1)分别求出a,b,x,y的值;
(2)从第2,3,4组回答正确的人中用分层抽样的方法抽取6人,则第2,3,4组每组应各抽取多少人?
(3)在(2)的前提下,电视台决定在所抽取的6人中随机抽取3人颁发幸运奖,求:所抽取的人中第3组至少有1人获得幸运奖的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sinxcos2x,下列结论正确的是( )
A.y=f(x)的图象关于 ![]() 对称
对称
B.y=f(x)的图象关于 ![]() 对称
对称
C.y=f(x)的图象关于y轴对称
D.y=f(x)不是周期函数
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() 在(﹣1,+∞)是增函数.
在(﹣1,+∞)是增函数.
(1)当b=1时,求a的取值范围.
(2)若g(x)=f(x)﹣1008没有零点,f(1)=0,求f(﹣3)的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,设椭圆的中心为原点O,长轴在x轴上,上顶点为A,左、右焦点分别为F1 , F2 , 线段OF1 , OF2的中点分别为B1 , B2 , 且△AB1B2是面积为4的直角三角形.过B1作l交椭圆于P、Q两点,使PB2垂直QB2 , 求直线l的方程 . 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知{an}是等差数列,Sn是其前n项和.已知a1+a3=16,S4=28.
(1)求数列{an}的通项公式
(2)当n取何值时Sn最大,并求出这个最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an},{bn}满足a1=1,a2=2,b1=2,且对任意的正整数i,j,k,l,当i+j=k+l时,都有ai+bj=ak+bl , 则 ![]() 的值是( )
的值是( )
A.2012
B.2013
C.2014
D.2015
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com