某校要组建明星篮球队,需要在各班选拔预备队员,规定投篮成绩A级为入围选手,选拔过程中每人投篮5次,若投中3次确定为B级,若投中4次以上可确定为A级,已知某班同学阿明每次投篮投中的概率为0.5.
(1)求阿明投篮4次才被确定为B级的概率;
(2)设阿明投篮投中的次数为X,求X的分布表及期望;
(3)若连续两次投篮不中则停止投篮,求阿明不能入围的概率.
分析:(1)由选拔过程中每人投篮5次,若投中3次确定为B级,若投中4次以上可确定为A级,已知某班同学阿明每次投篮投中的概率为0.5.则阿明投篮4次才被确定为B级的事件为前3次投篮中有两次投中,一次未中,第四次也未投中,代入计算即可得到答案.
(2)由于投球5次,投中的次数X可能取值为0,1,2,3,4,5,我们分别计算P(X=0),P(X=1),P(X=2),P(X=3),P(X=4),P(X=5)的值,易得求X的分布表进而得到数学期望.
(3)若连续两次投篮不中则停止投篮,则阿明不能入围的事件分为以下几种情况:①5次投中3次,有C42+1种投球方式,
②投中2次,分别是中中否否、中否中否否、否中中否否、否中否中否,③投中1次分别有中否否、否中否否,④投中0次只有否否一种,分别计算即可得到答案.
解答:解:(1)阿明投篮4次才被确定为B级的概率
P=()2××=.(2分)
(2)由已知
x~B(5,),X的分布列为:
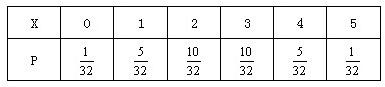 E(X)=
E(X)=.(4分)
(3)若连续两次投篮不中则停止投篮,
阿明不能入围这一事件有如下几种情况:
①5次投中3次,有C
42+1种投球方式,
其概率为
P(3)=(+1)()5=;(5分)
②投中2次,分别是中中否否、
中否中否否、否中中否否、否中否中否,
概率是:
P(2)=()4+3×()5=;(7分)
③投中1次分别有中否否、否中否否,
概率为:
P(1)=()3+()4=10;(8分)
④投中0次只有否否一种,
概率为
P(0)=()2=;(9分)
所以阿明不能入围这一事件的概率是:
P=P(3)+P(2)+P(1)+P(0)=.(10分)
点评:本小题主要考查相互独立事件概率的计算,运用数学知识解决问题的能力,要想计算一个事件的概率,首先我们要分析这个事件是分类的(分几类)还是分步的(分几步),然后再利用加法原理和乘法原理进行求解.对于概率要多练习使用列举法表示满足条件的基本事件个数.对于数学期望的计算则要熟练掌握运算方法和步骤.




 备战中考寒假系列答案
备战中考寒假系列答案