
(2006
湖南,18)如下图,已知两个正四棱锥P-ABCD与Q-ABCD的高分别为1和2,AB=4.(1)
证明:PQ⊥平面ABCD;(2)
求异面直线AQ与PB所成的角;(3)
求点P到平面QAD的距离.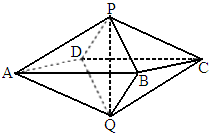
|
解析: (1)连结AC、BD,设AC∩BD=O,因为P-ABCD与Q-ABCD都是正四棱锥,所以PO⊥平面ABCD,QO⊥平面AB-CD,从而P、O、Q三点在一条直线上,所以PQ⊥平面ABCD.(2) 由题设知,ABCD是正方形,所以AC⊥BD.由 (1)知,PQ⊥平面ABCD,故可分别以直线CA、DB、QP为x轴、y轴、z轴建立空间直角坐标系(如图),由题设条件,相关各点的坐标分别是P(0,0,1),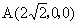 ,Q(0,0,-2), ,Q(0,0,-2), . .
所以  , ,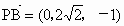 . .
于是 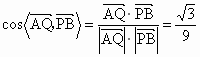 . .
从而异面直线 AQ与PB所成的角是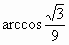 . .
(3) 由(2)知,点D的坐标是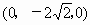 , ,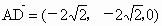 , ,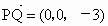 , ,
设 n=(x,y,z)是平面QAD的一个法向量,由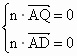 得 得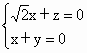 . .
取 x=1,得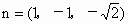 . .
所以点 P到平面QAD的距离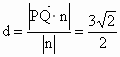 . . |


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com