
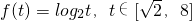
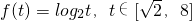 ,
, 即
即 ,
,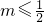 时
时 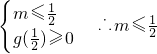
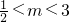 时
时 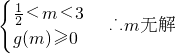
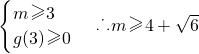
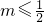 或
或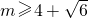 .
.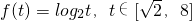 的单调性可求其值域G;
的单调性可求其值域G;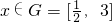 ,不等式-x2+2mx-m2+2m≤1恒成立可转化为x2-2mx+m2-2m+1≥0恒成立(
,不等式-x2+2mx-m2+2m≤1恒成立可转化为x2-2mx+m2-2m+1≥0恒成立( ),令g(x)=x2-2mx+m2-2m+1,其对称轴x=m,分区间在对称轴左侧(包括边界),右侧(包括边界),对称轴穿过
),令g(x)=x2-2mx+m2-2m+1,其对称轴x=m,分区间在对称轴左侧(包括边界),右侧(包括边界),对称轴穿过 ,三种情况利用函数的单调性及最值讨论解决.
,三种情况利用函数的单调性及最值讨论解决.

科目:高中数学 来源:2012-2013学年广东省深圳实验学校高三(上)数学周末练习(九)(解析版) 题型:解答题

 上恒成立,求实数m的取值范围.
上恒成立,求实数m的取值范围.查看答案和解析>>
科目:高中数学 来源:2010-2011学年广东省肇庆市高一(上)期末数学试卷(解析版) 题型:解答题

查看答案和解析>>
科目:高中数学 来源:2010年重庆市求精中学高考数学一模试卷(理科)(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com