
已知椭圆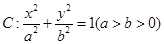 的离心率为
的离心率为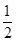 ,且过点
,且过点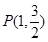 ,
, 为其右焦点.
为其右焦点.
(1)求椭圆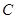 的方程;
的方程;
(2)设过点 的直线
的直线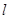 与椭圆相交于
与椭圆相交于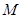 、
、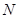 两点(点
两点(点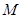 在
在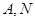 两点之间),若
两点之间),若 与
与 的面积相等,试求直线
的面积相等,试求直线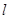 的方程.
的方程.
(1)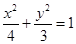 ;(2)
;(2)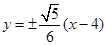 。
。
【解析】
试题分析:(1)因为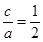 ,所以
,所以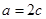 ,
,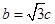 .
.
设椭圆方程为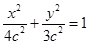 ,又点
,又点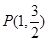 在椭圆上,所以
在椭圆上,所以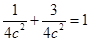 ,
,
解得 ,
,
所以椭圆方程为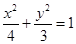 .
.
(2)易知直线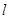 的斜率存在,
的斜率存在,
设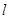 的方程为
的方程为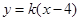 , 由
, 由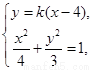 消去
消去 整理,得
整理,得
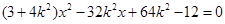 ,
,
由题意知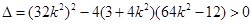 ,
,
解得 .
.
设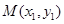 ,
,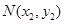 ,则
,则 , ①,
, ①,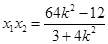 . ②.
. ②.
因为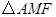 与
与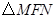 的面积相等,
的面积相等,
所以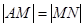 ,所以
,所以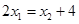 . ③ 由①③消去
. ③ 由①③消去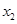 得
得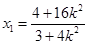 . ④
. ④
将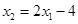 代入②得
代入②得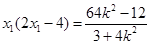 . ⑤
. ⑤
将④代入⑤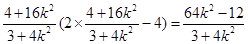 ,
,
整理化简得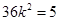 ,解得
,解得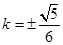 ,经检验成立.
,经检验成立.
所以直线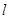 的方程为
的方程为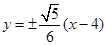 .
.
考点:椭圆的标准方程;椭圆的简单性质;直线与椭圆的综合应用。
点评:本题考查了椭圆方程的求法,以及直线与椭圆的综合应用,为圆锥曲线的常规题,应当掌握。考查了学生综合分析问题、解决问题的能力,知识的迁移能力以及运算能力。解题时要认真审题,仔细分析。


 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案科目:高中数学 来源: 题型:
A、
| ||||
B、
| ||||
C、
| ||||
| D、以上均不对 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,在由圆O:x2+y2=1和椭圆C:
如图,在由圆O:x2+y2=1和椭圆C:| x2 |
| a2 |
| ||
| 3 |
| OA |
| OB |
| 1 |
| 2 |
| OM |
查看答案和解析>>
科目:高中数学 来源: 题型:
| ||
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,A,B是椭圆C:
如图,A,B是椭圆C:| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com