
【题目】篮球运动于1891年起源于美国,它是由美国马萨诸塞州斯普林菲尔德(旧译麻省春田)市基督教青年会(![]() )训练学校的体育教师詹姆士·奈史密斯博士(
)训练学校的体育教师詹姆士·奈史密斯博士(![]() )发明.它是以投篮、上篮和扣篮为中心的对抗性体育运动之一,是可以增强体质的一种运动.已知篮球的比赛中,得分规则如下:3分线外侧投入可得3分,3分线内侧投入可得2分,不进得0分.经过多次试验,某人投篮100次,有20个是3分线外侧投入,30个是3分线内侧投入,其余不能入篮,且每次投篮为相互独立事件.
)发明.它是以投篮、上篮和扣篮为中心的对抗性体育运动之一,是可以增强体质的一种运动.已知篮球的比赛中,得分规则如下:3分线外侧投入可得3分,3分线内侧投入可得2分,不进得0分.经过多次试验,某人投篮100次,有20个是3分线外侧投入,30个是3分线内侧投入,其余不能入篮,且每次投篮为相互独立事件.
(1)求该人在4次投篮中恰有三次是3分线外侧投入的概率;
(2)求该人在4次投篮中至少有一次是3分线外侧投入的概率;
(3)求该人两次投篮后得分![]() 的分布列及数学期望.
的分布列及数学期望.
【答案】(1) ![]() (2)
(2) ![]() (3)见解析
(3)见解析
【解析】
(1)由古典概型概率公式求出“3分线外侧投入”的概率,利用独立重复实验概率公式求解即可;(2)利用独立事件的概率公式,结合对立事件的概率公式求解即可;(3)两次投篮后得分的得分可能取值为0,2,3,4,5,6,独立事件与互斥事件概率公式求出各随机变量对应的概率,从而可得分布列,进而利用期望公式可得![]() 的数学期望.
的数学期望.
“3分线外侧投入”“3分线内侧投入”“不能入篮”分别记为事件![]() ,
,![]() ,
,![]() ,则由题意知:
,则由题意知:![]() ,
,![]() ,
,![]() .
.
(1)因为每次投篮为相互独立事件,故4次投篮中恰有三次是3分线外侧投入的概率为
![]() .
.
(2)记“该人在4次投篮中至少有一次是3分线外侧投入”为事件![]() ,则“该人在4次投篮中没有一次是3分线外侧投入”为事件
,则“该人在4次投篮中没有一次是3分线外侧投入”为事件![]() .
.
易知![]() ,
,
则![]() .
.
即该人在4次投篮中至少有一次是3分线外侧投入的概率为![]() .
.
(3)两次投篮后得分的得分可能取值为0,2,3,4,5,6,
由于该人两次投篮互不影响,是相互独立事件,
![]() 表示两次投篮都不能入篮,则
表示两次投篮都不能入篮,则![]() ;
;
![]() 表示一次是3分线内侧投入,另一次不能入篮,则
表示一次是3分线内侧投入,另一次不能入篮,则![]() ;
;
![]() 表示一次是3分线外侧投入,另一次不能入篮,则
表示一次是3分线外侧投入,另一次不能入篮,则![]() ;
;
![]() 表示两次都是3分线内侧投入,则
表示两次都是3分线内侧投入,则![]() ;
;
![]() 表示一次是3分线外侧投入,另一次是3分线内侧投入,则
表示一次是3分线外侧投入,另一次是3分线内侧投入,则![]() ;
;
![]() 表示两次都是3分线外侧投入,则
表示两次都是3分线外侧投入,则![]() .
.
所以![]() 的分布列为
的分布列为
| 0 | 2 | 3 | 4 | 5 | 6 |
P |
|
|
|
|
|
|
数学期望为![]() .
.


 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案科目:高中数学 来源: 题型:
【题目】海洋蓝洞是地球罕见的自然地理现象,被喻为“地球留给人类保留宇宙秘密的最后遗产”,我国拥有世界上最深的海洋蓝洞,若要测量如图所示的蓝洞的口径![]() ,
,![]() 两点间的距离,现在珊瑚群岛上取两点
两点间的距离,现在珊瑚群岛上取两点![]() ,
,![]() ,测得
,测得![]() ,
,![]() ,
,![]() ,
,![]() ,则
,则![]() ,
,![]() 两点的距离为___.
两点的距离为___.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知长方形ABCD中,![]() ,
,![]() ,M为DC的中点,将
,M为DC的中点,将![]() 沿AM折起,使得平面
沿AM折起,使得平面![]() 平面ABCM.
平面ABCM.
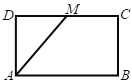
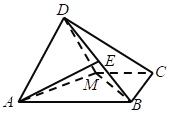
(1)求证:平面![]() 平面BMD;
平面BMD;
(2)若点E是线段DB上的一动点,问![]() 为何值时,二面角
为何值时,二面角![]() 的余弦值为
的余弦值为![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 过点
过点 和点
和点![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)设直线![]() 与椭圆
与椭圆![]() 相交于不同的两点
相交于不同的两点![]() ,
, ![]() ,是否存在实数
,是否存在实数![]() ,使得
,使得![]() ?若存在,求出实数
?若存在,求出实数![]() ;若不存在,请说明理由.
;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】十二生肖的座位次序如下图1,中间的狗、猪位置固定不动,其他生肖动物每次顺时针转动一格,即第一次转动后的座位次序如下图2,这样继续进行下去,那么第2019次换座位后,鼠的座位对应的编号为________.
图一:
鼠1 | 牛2 | 虎3 | 兔4 |
鸡10 | 狗11 | 猪12 | 龙5 |
猴9 | 羊8 | 马7 | 蛇6 |
图二:
鸡1 | 鼠2 | 牛3 | 虎4 |
猴10 | 狗11 | 猪12 | 兔5 |
羊9 | 马8 | 蛇7 | 龙6 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在长方体ABCD﹣A1B1C1D1,若AB=BC,E,F分别是AB1,BC1的中点,则下列结论中不成立的是( )

A.EF与BB1垂直B.EF⊥平面BDD1B1
C.EF与C1D所成的角为45°D.EF∥平面A1B1C1D1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,近日我渔船编队在岛![]() 周围海域作业,在岛
周围海域作业,在岛![]() 的南偏西20°方向有一个海面观测站
的南偏西20°方向有一个海面观测站![]() ,某时刻观测站发现有不明船只向我渔船编队靠近,现测得与
,某时刻观测站发现有不明船只向我渔船编队靠近,现测得与![]() 相距31海里的
相距31海里的![]() 处有一艘海警船巡航,上级指示海警船沿北偏西40°方向,以40海里/小时的速度向岛
处有一艘海警船巡航,上级指示海警船沿北偏西40°方向,以40海里/小时的速度向岛![]() 直线航行以保护我渔船编队,30分钟后到达
直线航行以保护我渔船编队,30分钟后到达![]() 处,此时观测站测得
处,此时观测站测得![]() 间的距离为21海里.
间的距离为21海里.

(Ⅰ)求![]() 的值;
的值;
(Ⅱ)试问海警船再向前航行多少分钟方可到岛![]() ?
?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com