Question

在数列{a_n}中，a₁=1，a₂=3，a_n+2=3a_n+1-2a_n，n∈N^*．
（Ⅰ）求a₃，a₄的值；
（Ⅱ）写出输入n（n≥3）值，输出a₁，a₂，…，a_n值的算法，并画出该算法的程序框图；
（Ⅲ）根据（Ⅱ）中的算法及框图，编写一个输入n值，输出a₁，a₂，…，a_n值的计算机程序．

Answer 1

解：（Ⅰ）因为a₁=1，a₂=3，a_n+2=3a_n+1-2a_n，n∈N^*，
所以a₃=3×a₂-2×a₁=7，a₄=3×a₃-2×a₂=15．　　　（2分）
（Ⅱ）算法如下：
第一步，输入一个n值．
第二步，初始化变量a，b，i，让a=1，b=3，i=3，并输出a，b．
第三步，计算c=3b-2a，并让a=b，b=c，i=i+1，输出c．
第四步，判断i＞n是否成立，若否，返回第三步；若是，结束算法． （6分）
算法程序框图为：
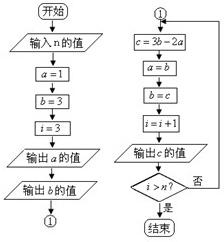
（10分）
（Ⅲ）程序设计：
（12分）
分析：（I）由已知中a₁=1，a₂=3，a_n+2=3a_n+1-2a_n，n∈N^*，我们分别令n=1，n=2代入即可计算出a₃，a₄的值；
（Ⅱ）根据已知中的递推公式，我们可以得到一个利用循环计算并输出a₁，a₂，…，a_n值的算法，包括输入n，a，b，i等变量的值，其中a，b指数列的前两项，利用循环递推计算并输出a₃，a₄，…，a_n值，进而可画出该算法的程序框图；
（Ⅲ）根据（II）中所得的算法的程序框图，结合框图中各种框对应的程序语句，可以编写出输入n值，输出a₁，a₂，…，a_n值的计算机程序．
点评：本题考查的知识点是设计程序框图解决实际问题，数列的递推式，循环语句，其中熟练掌握循环结构的特点及与循环语句的对应关系是解答本题的关键．