若函数f(x)定义域为R,满足对任意x1,x2∈R,有f(x1+x2)≤f(x1)+f(x2),则称f(x)为“V形函数”;若函数g(x)定义域为R,g(x)恒大于0,且对任意x1,x2∈R,有lgg(x1+x2)≤lgg(x1)+lgg(x2),则称g(x)为“对数V形函数”.
(1)当f(x)=x2时,判断f(x)是否为V形函数,并说明理由;
(2)当g(x)=x2+2时,证明:g(x)是对数V形函数;
(3)若f(x)是V形函数,且满足对任意x∈R,有f(x)≥2,问f(x)是否为对数V形函数?证明你的结论.
(1)解:f(x
1+x
2)-[f(x
1)+f(x
2)]=(x
1+x
2)
2-(

+

)=2x
1x
2∵x
1,x
2∈R,∴2x
1x
2符号不定,∴当2x
1x
2≤0时,f(x)是V形函数;当2x
1x
2>0时,f(x)不是V形函数;
(2)证明:假设对任意x
1,x
2∈R,有lgg(x
1+x
2)≤lgg(x
1)+lgg(x
2),
则lgg(x
1+x
2)-lgg(x
1)-lgg(x
2)=lg[(x
1+x
2)
2+2]-lg(x
12+2)-lg(x
22+2)≤0,
∴(x
1+x
2)
2+2≤(x
12+2)(x
22+2),
∴x
12x
22+(x
1-x
2)
2+2≥0,显然成立,
∴假设正确,g(x)是对数V形函数;
(3)解:f(x)是对数V形函数
证明:∵f(x)是V形函数,∴对任意x
1,x
2∈R,有f(x
1+x
2)≤f(x
1)+f(x
2),
∵对任意x∈R,有f(x)≥2,∴
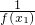
+
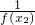
≤1,∴0<f(x
1)+f(x
2)≤f(x
1)f(x
2),
∴f(x
1+x
2)≤f(x
1)f(x
2),
∴lgf(x
1+x
2)≤lgf(x
1)+lgf(x
2),
∴f(x)是对数V形函数.
分析:(1)由f(x
1+x
2)-[f(x
1)+f(x
2)]=(x
1+x
2)
2-(

+

)=2x
1x
2,可得2x
1x
2符号不定,从而可得结论;
(2)利用反证法证明.假设对任意x
1,x
2∈R,有lgg(x
1+x
2)≤lgg(x
1)+lgg(x
2),则可得(x
1+x
2)
2+2≤(x
12+2)(x
22+2),即证x
12x
22+(x
1-x
2)
2+2≥0,显然成立;
(3)f(x)是对数V形函数,根据f(x)是V形函数,利用对任意x∈R,有f(x)≥2,证明f(x
1+x
2)≤f(x
1)f(x
2),从而可得f(x)是对数V形函数.
点评:本题考查新定义,考查学生分析解决问题的能力,解题的关键是正确理解新定义.

 +
+ )=2x1x2
)=2x1x2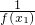 +
+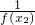 ≤1,∴0<f(x1)+f(x2)≤f(x1)f(x2),
≤1,∴0<f(x1)+f(x2)≤f(x1)f(x2), +
+ )=2x1x2,可得2x1x2符号不定,从而可得结论;
)=2x1x2,可得2x1x2符号不定,从而可得结论;

 名校课堂系列答案
名校课堂系列答案