有穷数列{an}的前n项和Sn=2n2+n,现从中抽取某一项(不包括首项、末项)后,余下的项的平均值是79.
①求数列{an}的通项an;
②求这个数列的项数,抽取的是第几项?
【答案】
分析:①由已知中数列{a
n}的前n项和S
n=2n
2+n,根据a
n=S
n-S
n-1可求出当n≥2时,数列{a
n}的通项a
n,验证n=1,a
1=S
1=3后,即可得到数列{a
n}的通项a
n;
②设抽取的是第k项,由现从中抽取某一项(不包括首项、末项)后,余下的项的平均值是79,可以构造关于k的方程,解方程即可求出k值.
解答:解:①由S
n=2n
2+n得a
1=S
1=3,当n≥2时,a
n=S
n-S
n-1=4n-1,显然满足n=1,
∴a
n=4n-1,
∴数列{a
n}是公差为4的递增等差数列.
②设抽取的是第k项,则S
n-a
k=79(n-1),a
k=(2n
2+n)-79(n-1)=2n
2-78n+79.
由
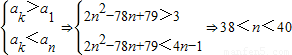
,∵n∈N
*,∴n=39,
由a
k=2n
2-78n+79=2×39
2-78×39+79=4k-1⇒k=20.
故数列{a
n}共有39项,抽取的是第20项.
点评:本题考查的知识点是等差数列的通项公式,其中a
n=S
n-S
n-1是由数列{a
n}的前n项和求数列{a
n}的通项a
n最常用的方法,要注意对n=1时,a
1=S
1的验证.

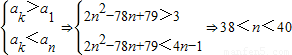 ,∵n∈N*,∴n=39,
,∵n∈N*,∴n=39,

 阅读快车系列答案
阅读快车系列答案