
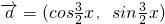 ,
,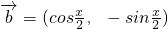 ,x
,x .
. 及|
及| |;
|;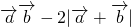 值域.
值域. =cos
=cos x•cos
x•cos x-sin
x-sin x•sin
x•sin x=cos(
x=cos( x+
x+ x)=cos2x.
x)=cos2x. )2=(cos
)2=(cos x+cos
x+cos x)2+(sin
x)2+(sin x-sin
x-sin x)2=2+2(cos
x)2=2+2(cos x•cos
x•cos x-sin
x-sin x•sin
x•sin x)
x) ]
] |=2cosx.
|=2cosx.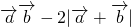 =cos2x-4cosx
=cos2x-4cosx ]∴cosx∈[0,1]
]∴cosx∈[0,1]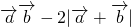 值域是[-3,-1].
值域是[-3,-1]. •
• ;因为|
;因为| |2=(
|2=( )2,所以先求(
)2,所以先求( )2,然后求|
)2,然后求| |.
|. •
• 与|
与| |求出f(x),然后把它整理为二次函数形式,进而结合余弦的值域解决问题.
|求出f(x),然后把它整理为二次函数形式,进而结合余弦的值域解决问题.

 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案科目:高中数学 来源: 题型:
| a |
| π |
| 4 |
| b |
| 2 |
| a |
| b |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| a |
| π |
| 4 |
| b |
| a |
| b |
| π |
| 4 |

查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题共12分)
在平面直角坐标系中,已知向量a=(![]() x,y+1),向量b=(x,y—1),a⊥b,动点M
x,y+1),向量b=(x,y—1),a⊥b,动点M
(x,y)的轨迹为E。
(Ⅰ)证明:存在圆心在原点的圆,使得该圆的任意一条切线与轨迹E恒有两个交点
A、B,且OA⊥OB(O为坐标原点),并求出该圆的方程;
(Ⅱ)设直线l与圆C:x![]() +y
+y![]() =R
=R![]() (1<R<2)相切于A
(1<R<2)相切于A![]() ,且l与轨迹E只有一个
,且l与轨迹E只有一个
公共点B![]() ,当R为何值时,| A
,当R为何值时,| A![]() B
B![]() |取得最大值?并求出最大值。
|取得最大值?并求出最大值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com