
甲、乙二射击运动员分别对一目标射击![]() 次,甲射中的概率为
次,甲射中的概率为![]() ,乙射中的概率为
,乙射中的概率为![]() ,求:
,求:
(1)![]() 人都射中目标的概率;
人都射中目标的概率;
(2)![]() 人中恰有
人中恰有![]() 人射中目标的概率;
人射中目标的概率;
(3)![]() 人至少有
人至少有![]() 人射中目标的概率;
人射中目标的概率;
(4)![]() 人至多有
人至多有![]() 人射中目标的概率?
人射中目标的概率?
(1)![]() (2)
(2)![]() (3)
(3)![]() (4)
(4)![]()
记“甲射击![]() 次,击中目标”为事件
次,击中目标”为事件![]() ,“乙射击
,“乙射击![]() 次,击中目标”为事件
次,击中目标”为事件![]() ,则
,则![]() 与
与![]() ,
,![]() 与
与![]() ,
,![]() 与
与![]() ,
,![]() 与
与![]() 为相互独立事件,
为相互独立事件,
(1)![]() 人都射中的概率为:
人都射中的概率为:
![]() ,
,
∴![]() 人都射中目标的概率是
人都射中目标的概率是![]() .
.
(2)“![]() 人各射击
人各射击![]() 次,恰有
次,恰有![]() 人射中目标”包括两种情况:一种是甲击中、乙未击中(事件
人射中目标”包括两种情况:一种是甲击中、乙未击中(事件![]() 发生),另一种是甲未击中、乙击中(事件
发生),另一种是甲未击中、乙击中(事件![]() 发生)
发生)![]() 根据题意,事件
根据题意,事件![]() 与
与![]() 互斥,根据互斥事件的概率加法公式和相互独立事件的概率乘法公式,所求的概率为:
互斥,根据互斥事件的概率加法公式和相互独立事件的概率乘法公式,所求的概率为:
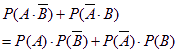
![]()
∴![]() 人中恰有
人中恰有![]() 人射中目标的概率是
人射中目标的概率是![]() .
.
(3)(法1):2人至少有1人射中包括“2人都中”和“2人有1人不中”2种情况,其概率为![]() .
.
(法2):“2人至少有一个击中”与“2人都未击中”为对立事件,
2个都未击中目标的概率是![]() ,
,
∴“两人至少有1人击中目标”的概率为![]() .
.
(4)(法1):“至多有1人击中目标”包括“有1人击中”和“2人都未击中”,
故所求概率为:
![]()
![]()
![]() .
.
(法2):“至多有1人击中目标”的对立事件是“2人都击中目标”,
故所求概率为![]()
![]()


科目:高中数学 来源:广东省惠州市2012届高三第一次调研考试文科数学 题型:解答题
(本小题满分12分)
甲、乙二名射击运动员参加今年深圳举行的第二十六届世界大学生夏季运动会的预选赛,他们分别射击了4次,成绩如下表(单位:环):
| 甲 | 5 | 6 | 9 | 10 |
| 乙 | 6 | 7 | 8 | 9 |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年广东省高三上学期期中考试文科数学试卷(解析版) 题型:解答题
(本小题满分12分)
甲、乙二名射击运动员参加今年深圳举行的第二十六届世界大学生夏季运动会的预选赛,他们分别射击了4次,成绩如下表(单位:环):
|
甲 |
5 |
6 |
9 |
10 |
|
乙 |
6 |
7 |
8 |
9 |
(1)从甲、乙两人的成绩中各随机抽取一个,求甲的成绩比乙高的概率;
(2)现要从中选派一人参加决赛,你认为选派哪位运动员参加比较合适?请说明理由.
查看答案和解析>>
科目:高中数学 来源:广东省惠州市2011-2012学年高三第一次调研考试文科数学 题型:解答题
(本小题满分12分)
甲、乙二名射击运动员参加今年深圳举行的第二十六届世界大学生夏季运动会的预选赛,他们分别射击了4次,成绩如下表(单位:环):
|
甲 |
5 |
6 |
9 |
10 |
|
乙 |
6 |
7 |
8 |
9 |
(1)从甲、乙两人的成绩中各随机抽取一个,求甲的成绩比乙高的概率;
(2)现要从中选派一人参加决赛,你认为选派哪位运动员参加比较合适?请说明理由.
查看答案和解析>>
科目:高中数学 来源:2013届广东省湛江市高二第一学期期末考试文科数学 题型:解答题
(本小题满分12分)甲、乙二名射击运动员参加第二十六届世界大学生夏季运动会的预选赛,他们分别射击了4次,成绩如下表(单位:环):
|
甲 |
5 |
6 |
9 |
10 |
|
乙 |
6 |
7 |
8 |
9 |
(1)从甲、乙两人的成绩中各随机抽取一个,求甲的成绩比乙高的概率;
(2)现要从中选派一人参加决赛,你认为选派哪位运动员参加比较合适?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题14分) (以下二题选做其一)
(1)甲乙两运动员进行射击训练,已知他们击中的环数都稳定在![]() 环内,且每次射击成绩互不影响,射击环数的频率分布条形图如下图所示,若将频率视为概率,回答下列问题.
环内,且每次射击成绩互不影响,射击环数的频率分布条形图如下图所示,若将频率视为概率,回答下列问题.
(Ⅰ)求甲运动员在一次射击中击中![]() 环以上(含
环以上(含![]() 环)的概率;
环)的概率;
(Ⅱ)求甲运动员在![]() 次射击中至少有
次射击中至少有![]() 次击中
次击中![]() 环以上(含
环以上(含![]() 环)的概率;
环)的概率;
(Ⅲ)若甲、乙两运动员各射击![]() 次,
次,![]() 表示这
表示这![]() 次射击中击中
次射击中击中![]() 环以上(含
环以上(含![]() 环)的次数,求
环)的次数,求![]() 的分布列及
的分布列及![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com