
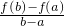 (x-a)|≤T(T为常数)成立,则称函数f(x)在[a,b]上具有“T级线性逼近”.下列函数中:
(x-a)|≤T(T为常数)成立,则称函数f(x)在[a,b]上具有“T级线性逼近”.下列函数中: ;
; 级线性逼近”的函数的个数为
级线性逼近”的函数的个数为 级线性逼近”的定义,从而得出结论.
级线性逼近”的定义,从而得出结论.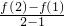 (x-1)|=|0|≤
(x-1)|=|0|≤ ,故f(x)=2x+1在区间[1,2]上具有“
,故f(x)=2x+1在区间[1,2]上具有“ 级线性逼近”,故满足条件.
级线性逼近”,故满足条件.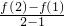 (x-1)|=|(x-1)(x-2)|=-(x-1)(x-2)≤
(x-1)|=|(x-1)(x-2)|=-(x-1)(x-2)≤ ,
, 级线性逼近”,故满足条件.
级线性逼近”,故满足条件. 在区间[1,2]上,由于|f(x)-f(1)-
在区间[1,2]上,由于|f(x)-f(1)-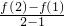 (x-1)|=|
(x-1)|=| +
+ -
- |=
|= -(
-( +
+ )≤
)≤ -2
-2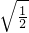 =
= -
- ≤
≤ ,
, 级线性逼近”,故满足条件.
级线性逼近”,故满足条件.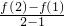 (x-1)|=|x3-7x+6|=|(x-1)(x-3)(x+2)|=-(x-1)(x-3)(x+2),
(x-1)|=|x3-7x+6|=|(x-1)(x-3)(x+2)|=-(x-1)(x-3)(x+2),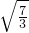 ,在[1,
,在[1,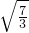 ]上,3x2-7<0,-(x-1)(x-3)(x+2)为增函数,
]上,3x2-7<0,-(x-1)(x-3)(x+2)为增函数,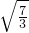 ,2]上,-(x-1)(x-3)(x+2)为减函数,故-(x-1)(x-3)(x+2)的最大值为 (
,2]上,-(x-1)(x-3)(x+2)为减函数,故-(x-1)(x-3)(x+2)的最大值为 (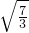 -1)(3-
-1)(3-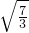 )(
)(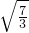 +2)>
+2)> ,
, 级线性逼近”,故不满足条件.
级线性逼近”,故不满足条件.

 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案科目:高中数学 来源: 题型:
| x1+x2 |
| 2 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| x1+x2 |
| 2 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年黑龙江省大庆市铁人中学高三(上)第二次段考数学试卷(解析版) 题型:选择题
 ,3},则使函数y=xa的定义域为R且该函数为奇函数的所有a的值为1,3;
,3},则使函数y=xa的定义域为R且该函数为奇函数的所有a的值为1,3;查看答案和解析>>
科目:高中数学 来源:2012-2013学年湖北省襄阳市高一(上)期末数学试卷(解析版) 题型:解答题
 )>
)> [f(x1)+f(x2)],则称f(x)为定义域上的凸函数.
[f(x1)+f(x2)],则称f(x)为定义域上的凸函数.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com