
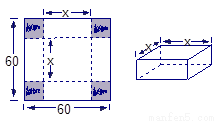
(本题8分)在边长为60 cm的正方形铁片的四角切去相等的正方形,再把它的边沿虚线折起(如图),做成一个无盖的方底箱子,箱底的边长是多少时,箱底的容积最大?最大容积是多少?
科目:高中数学 来源: 题型:
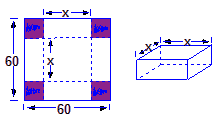
(本题8分)在边长为60 cm的正方形铁片的四角切去相等的正方形,再把它的边沿虚线折起(如图),做成一个无盖的方底箱子,箱底的边长是多少时,箱底的容积最大?最大容积是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
(本题满分14分)本题共有2个小题,第1小题满分6分,第2小题满分8分.
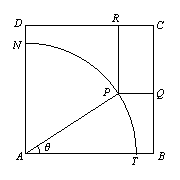
如图所示,ABCD是一块边长为7米的正方形铁皮,其中ATN是一半径为6米的扇形,已经被腐蚀不能使用,其余部分完好可利用.工人师傅想在未被腐蚀部分截下一个有边落在BC与CD上的长方形铁皮PQCR,其中P是![]() 上一点.设
上一点.设![]() ,长方形PQCR的面积为S平方米.
,长方形PQCR的面积为S平方米.
(1)求S关于![]() 的函数解析式;
的函数解析式;
(2)设![]() ,求S关于t的表达式以及S的最大值.
,求S关于t的表达式以及S的最大值.
 |
查看答案和解析>>
科目:高中数学 来源:2011届上海市卢湾区高三上学期期末数学理卷 题型:解答题
(本题满分14分)本题共有2个小题,第1小题满分6分,第2小题满分8分.
如图所示,ABCD是一块边长为7米的正方形铁皮,其中ATN是一半径为6米的扇形,已经被腐蚀不能使用,其余部分完好可利用.工人师傅想在未被腐蚀部分截下一个有边落在BC与CD上的长方形铁皮PQCR,其中P是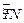
 上一点.设
上一点.设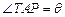 ,长方形PQCR的面积为S平方米.
,长方形PQCR的面积为S平方米.
(1)求S关于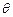 的函数解析式;
的函数解析式;
(2)设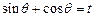 ,求S关于t的表达式以及S的最大值.
,求S关于t的表达式以及S的最大值.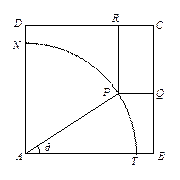
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com