
已知向量p=(an,2n),向量q=(2n+1,-an+1),n∈N*,向量p与q垂直,且a1=1.
(1)求数列{an}的通项公式;
(2)若数列{bn}满足bn=log2an+1,求数列{an·bn}的前n项和Sn.
(1) an=2n-1 (2) an·bn=n·2n-1 Sn=1+(n-1)2n
【解析】解:(1)∵向量p与q垂直,
∴2nan+1-2n+1an=0,即2nan+1=2n+1an,
∴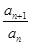 =2,∴{an}是以1为首项, 2为公比的等比数列,∴an=2n-1.
=2,∴{an}是以1为首项, 2为公比的等比数列,∴an=2n-1.
(2)∵bn=log2an+1,∴bn=n,
∴an·bn=n·2n-1,
∴Sn=1+2·2+3·22+4·23+…+n·2n-1,①
∴2Sn=1·2+2·22+3·23+4·24+…+n·2n,②
①-②得,
-Sn=1+2+22+23+24+…+2n-1-n·2n
=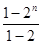 -n·2n=(1-n)2n-1,
-n·2n=(1-n)2n-1,
∴Sn=1+(n-1)2n.


科目:高中数学 来源:重难点手册 高中数学·必修4(配人教A版新课标) 人教A版新课标 题型:044
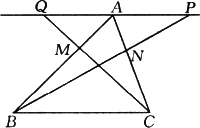
如下图,已知△ABC中,点N在AC上,且AN=![]() AC,M在AB上,且AM=
AC,M在AB上,且AM=![]() AB,在BN的延长线上取点P,使NP=
AB,在BN的延长线上取点P,使NP=![]() BN,在CM的延长线上取点Q,使MQ=
BN,在CM的延长线上取点Q,使MQ=![]() CM,用向量方法证明:P、A、Q三点共线.
CM,用向量方法证明:P、A、Q三点共线.
查看答案和解析>>
科目:高中数学 来源:贵州省遵义四中组团7校2011届高三第一次联考数学理科试题 题型:013
已知等差数列{an}的前n项和为Sn,且S2=10,S5=55,则过点P(n,an)(n∈N*)和Q(n+2,an+2)(n∈N*)的直线的一个方向向量坐标可以是
A.(2,4)
B.(-1,-1)
C.(-![]() ,-1)
,-1)
D.(-![]() ,-
,-![]() )
)
查看答案和解析>>
科目:高中数学 来源:2011-2012学年山西省高三2月月考文科数学试卷 题型:选择题
已知等差数列{an}的前n项的和为Sn,且S2=10,S5=55,则过点P(n,an)和Q(n+2,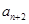 )(n∈N*)的直线的一个方向向量的坐标是
)(n∈N*)的直线的一个方向向量的坐标是
A、(2,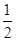 ) B、(-
) B、(-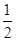 ,-2) C、(-
,-2) C、(-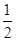 ,-1) D、(-1,-1)
,-1) D、(-1,-1)
查看答案和解析>>
科目:高中数学 来源: 题型:
已知等差数列{an}的前n项和为Sn,且S2=10,S5=55,则过点P(n,an)和Q(n+2,an+2)(n∈N+)的直线的一个方向向量的坐标可以是( )
(A)(2,4) (B)(-![]() ,-
,-![]() )
)
(C)(-![]() ,-1) (D)(-1,-1)
,-1) (D)(-1,-1)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com