
已知点P(3,4)是椭圆+=1(a>b>0)上的一点,F1、F2是椭圆的两焦点,若PF1⊥PF2,试求:
(1)椭圆方程;
(2)△PF1F2的面积.
解:(1)法一:令F1(-c,0),F2(c,0),
∵PF1⊥PF2,∴kPF1·kPF2=-1,………………3分
即·=-1,解得c=5,
∴椭圆方程为+=1.
∵点P(3,4)在椭圆上,
∴+=1,
解得a2=45或a2=5,
又a>c,∴a2=5舍去,
故所求椭圆方程为+=1.………………5分
法二:∵PF1⊥PF2,
∴△PF1F2为直角三角形,
∴|OP|=|F1F2|=c.
又|OP|==5,∴c=5,
∴椭圆方程为+=1(以下同法一).………………5分
(2)法一:P点纵坐标的值即为F1F2边上的高,
∴S△PF1F2=|F1F2|×4=×10×4=20.………………10分
法二:由椭圆定义知:|PF1|+|PF2|=6①
又|PF1|2+|PF2|2=|F1F2|2②
①2-②得2|PF1|·|PF2|=80,
∴S△PF1F2=|PF1|·|PF2|=20.………………10分
【解析】略


科目:高中数学 来源:2013-2014学年江西师大附中,临川一中高三期末联考理科数学试卷(解析版) 题型:选择题
已知点P(3,4)和圆C:(x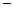 2)2+y2=4,A,B是圆C上两个动点,且|AB|=
2)2+y2=4,A,B是圆C上两个动点,且|AB|=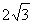 ,则
,则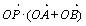 (O为坐标原点)的取值范围是( )
(O为坐标原点)的取值范围是( )
A.[3,9] B.[1,11] C.[6,18] D.[2,22]
查看答案和解析>>
科目:高中数学 来源:2013届黑龙江省高二期3月月考数学(理)试卷(解析版) 题型:解答题
已知点P(3,4)是椭圆+=1(a>b>0)上的一点,F1、F2是椭圆的两焦点,若PF1⊥PF2,试求:
(1)椭圆方程;
(2)△PF1F2的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知点P(3,4)是椭圆+=1(a>b>0)上的一点,F1、F2是椭圆的两焦点,若PF1⊥PF2,试求:
(1)椭圆方程;
(2)△PF1F2的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com