
在数列{an}中,a1=1,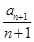 =
= +
+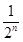 .
.
(1)设bn= ,求数列{bn}的通项公式;
,求数列{bn}的通项公式;
(2)求数列{an}的前n项和Sn.
(1) bn=2-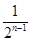 (2) n(n+1)+
(2) n(n+1)+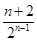 -4
-4
【解析】(1)由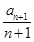 =
=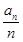 +
+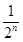 可知bn+1=bn+
可知bn+1=bn+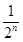 ,然后可利用叠加法求bn.
,然后可利用叠加法求bn.
(2)再利用bn=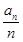 可求出
可求出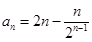 ,然后再利用分组求和和错位相减法求和即可.
,然后再利用分组求和和错位相减法求和即可.
解:(1)由已知得b1=a1=1且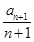 =
=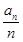 +
+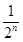 ,
,
即bn+1=bn+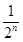 ,
,
从而b2=b1+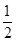 ,
,
b3=b2+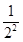 ,
,
…
bn=bn-1+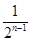 ( n≥2),
( n≥2),
于是bn=b1+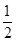 +
+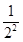 +…+
+…+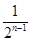 ,
,
=2-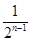 ( n≥2), ………………4分
( n≥2), ………………4分
又b1=1, ………………5分
∴{bn}的通项公式bn=2-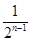 .………………6分
.………………6分
(2)由(1)知an=n·bn=2n-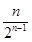 , ………………7分
, ………………7分
令Tn=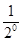 +
+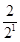 +
+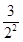 +…+
+…+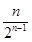 ,
,
则2Tn=2+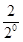 +
+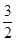 +…+
+…+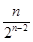 , ………………8分
, ………………8分
作差得:
Tn=2+(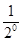 +
+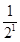 +…+
+…+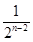 )-
)-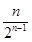 =4-
=4-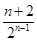 , ………………10分
, ………………10分
∴Sn=(2+4+6+…+2n)-Tn
=n(n+1)+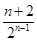 -4. ………………12分
-4. ………………12分
说明:各题如有其它解法可参照给分.


科目:高中数学 来源: 题型:
| 1 |
| 3 |
| 1 |
| an |
| an |
| n |
| 1 |
| 3 |
| 3 |
| 4 |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年广东省汕尾市陆丰市碣石中学高三(上)第四次月考数学试卷(理科)(解析版) 题型:解答题
 ,并且对任意n∈N*,n≥2都有an•an-1=an-1-an成立,令bn=
,并且对任意n∈N*,n≥2都有an•an-1=an-1-an成立,令bn= (n∈N*).
(n∈N*). }的前n项和为Tn,证明:
}的前n项和为Tn,证明: .
.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com