下列四组函数中表示同一函数的是（ ）
A． ， | B． |
C． ， | D． ， |
C
解析试题分析：要判断两个函数是否是同一个函数，需要从三个方面来分析，即定义域，对应法则和值域，观察四个选项结果有三个的定义域不同，只有选C．解：要判断两个函数是否是同一个函数，需要从三个方面来分析，即定义域，对应法则和值域，对于A选项，f（x）的定义域为R，g（x）的定义域为{x|x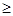
≠0}，∴不是同一函数．对于B选项，对应法则不同，∴不是同一函数，对于C选项，f（x）的定义域为R，g（x）的定义域为R，且两函数解析式化简后为同一解析式，∴是同一函数，对于D选项，f（x）的定义域为R，g（x）的定义域为x=1，∴不是同一函数,故选C．
考点：同一函数
点评：本题考查判断两个函数是否是同一函数，在开始学习函数的概念时，这是经常出现的一个问题，注意要从三个方面来分析．
科目：高中数学 来源： 题型：单选题
已知f（x）是以2为周期的偶函数，当x∈[0, 1]时，f（x）＝x，那么在区间[－1,3]内关于x的方程f（x）＝kx＋k＋1（k∈R，k≠－1）的根的个数
| A．不可能有3个 | B．最少有1个，最多有4个 |
| C．最少有1个，最多有3个 | D．最少有2个，最多有4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
的定义域为
，则函数
的定义域为（ ）
则不等式
的解集为（ ）
，+∞) 
的零点所在的大致区间是 （ ）
是方程
的解，则
是( )
的图象是（ ）
为奇函数,且当
时,
,则
( )
