解:(1)设f(x)=mx+n(m≠0),又f(3)=2,f(2)=3,
所以3m+n=2,2m+n=3?m=-1,n=5
即f(x)=-x+5?f(5)=0;
(2)①由
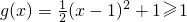
知g(x)在[a,b]上单调增函数且a≥1,
所以值域为[g(a),g(b)],
由已知
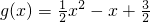
是[1,b]上的“方正”函数,所以[g(a),g(b)]=[a,b]
则g(a)=a,g(b)=b,即a,b是方程g(x)=x的两个根(1≤a<b)
解方程
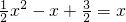
得x=1或x=3,所以a=1,b=3
②假设存在常数a,b,使函数
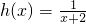
是区间[a,b]上的“方正”函数.
因a>-2,显然
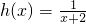
在区间[a,b]上是单调减函数,值域为[h(b),h(a)]=[a,b],
即
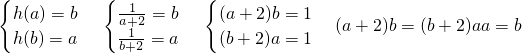
与a<b矛盾,
故不存在常数a,b,使函数
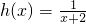
是区间[a,b]上的“方正”函数.
分析:(1)直接设出函数解析式,根据已知条件列出方程求出解析式即可得到结论.
(2))①先由
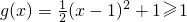
知g(x)在[a,b]上单调增函数且a≥1,再结合“方正”函数的定义得到g(a)=a,g(b)=b,即a,b是方程g(x)=x的两个根;解方程即可求出常数a,b的值.
②根据a>-2,得到
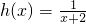
在区间[a,b]上是单调减函数,值域为[h(b),h(a)]=[a,b],解对应的方程组求出a=b与a<b矛盾即可得到结论.
点评:本题主要是在新定义下对函数单调性应用的考查,考查计算能力以及分析问题的能力.

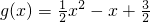 是[a,b]上的“方正”函数,求常数a,b的值.
是[a,b]上的“方正”函数,求常数a,b的值.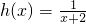 是区间[a,b]上的“方正”函数?若存在,求出a,b的值;不存在,说明理由.
是区间[a,b]上的“方正”函数?若存在,求出a,b的值;不存在,说明理由.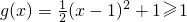 知g(x)在[a,b]上单调增函数且a≥1,
知g(x)在[a,b]上单调增函数且a≥1,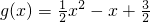 是[1,b]上的“方正”函数,所以[g(a),g(b)]=[a,b]
是[1,b]上的“方正”函数,所以[g(a),g(b)]=[a,b]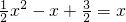 得x=1或x=3,所以a=1,b=3
得x=1或x=3,所以a=1,b=3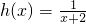 是区间[a,b]上的“方正”函数.
是区间[a,b]上的“方正”函数.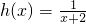 在区间[a,b]上是单调减函数,值域为[h(b),h(a)]=[a,b],
在区间[a,b]上是单调减函数,值域为[h(b),h(a)]=[a,b],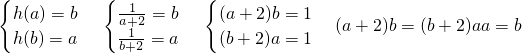 与a<b矛盾,
与a<b矛盾,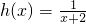 是区间[a,b]上的“方正”函数.
是区间[a,b]上的“方正”函数.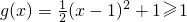 知g(x)在[a,b]上单调增函数且a≥1,再结合“方正”函数的定义得到g(a)=a,g(b)=b,即a,b是方程g(x)=x的两个根;解方程即可求出常数a,b的值.
知g(x)在[a,b]上单调增函数且a≥1,再结合“方正”函数的定义得到g(a)=a,g(b)=b,即a,b是方程g(x)=x的两个根;解方程即可求出常数a,b的值.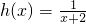 在区间[a,b]上是单调减函数,值域为[h(b),h(a)]=[a,b],解对应的方程组求出a=b与a<b矛盾即可得到结论.
在区间[a,b]上是单调减函数,值域为[h(b),h(a)]=[a,b],解对应的方程组求出a=b与a<b矛盾即可得到结论.

 名校课堂系列答案
名校课堂系列答案