
将一颗质地均匀的正方体骰子(六个面的点数分别为1,2,3,4,5,6)先后抛掷两次,将得到的点数分别记为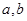 .
.
(1)求直线 与圆
与圆 相切的概率;
相切的概率;
(2)将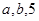 的值分别作为三条线段的长,求这三条线段能围成等腰三角形的概率.
的值分别作为三条线段的长,求这三条线段能围成等腰三角形的概率.
解:(1)1/2 (2) .
.
【解析】本试题主要考查了古典概型概率的运用。
解: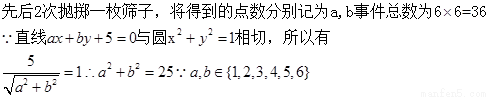
所以满足条件的的情况只有a=3,b=4,a=4,b=3两种,
所以直线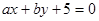 与圆
与圆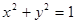 相切的概率1/2
相切的概率1/2
(2)先后2次抛掷一枚骰子,将得到的点数分别记为a,b,事件总数为6×6=36.
因为,三角形的一边长为5 所以,当a=1时,b=5,(1,5,5) 1种
当a=2时,b=5,(2,5,5) 1种
当a=3时,b=3,5,(3,3,5),(3,5,5) 2种
当a=4时,b=4,5,(4,4,5),(4,5,5) 2种
当a=5时,b=1,2,3,4,5,6,
(5,1,5),(5,2,5),(5,3,5),
(5,4,5),(5,5,5),(5,6,5) 6种
当a=6时,b=5,6,(6,5,5),(6,6,5) 2种
故满足条件的不同情况共有14种.
所以,三条线段能围成不同的等腰三角形的概率为 .
.


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com