Question

（20）如图，直线l₁：y＝kx（k>0）与直线l₂：y＝－kx之间的阴影区域（不含边界）记为W，其左半部分记为W₁，右半部分记为W₂.

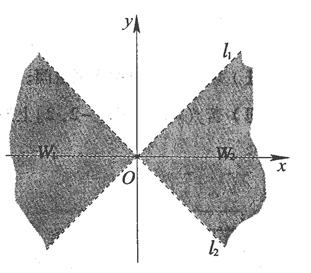
（Ⅰ）分别用不等式组表示W₁和W₂；

（Ⅱ）若区域W中的动点P(x，y)到l₁，l₂的距离之积等于d²，求点P的轨迹C的方程；

（Ⅲ）设不过原点O的直线l与（Ⅱ）中的曲线C相交于M₁，M₂两点，且与l₁，l₂分别交于M₃，M₄两点．求证△OM₁M₂的重心与△OM₃M₄的重心重合．

Answer 1

（20）解：（Ⅰ）W₁={(x, y)| kx<y<－kx，x<0}，

W₂={(x, y)|－kx＜y＜kx，x>0}，

（Ⅱ）直线l₁：kx－y＝0，直线l₂：kx＋y＝0，由题意得

,

即.

    由P(x，y)∈W，知k²x²－y²>0，

    所以，即.

所以动点P的轨迹C的方程为.

（Ⅲ）当直线l与x轴垂直时，可设直线l的方程为x＝a（a≠0）．由于直线l，曲线C关于x轴对称，且l₁与l₂关于x轴对称，于是M₁M₂，M₃M₄的中点坐标都为（a，0），所以△OM₁M₂，△OM₃M₄的重心坐标都为（，0），即它们的重心重合，

当直线l与x轴不垂直时，设直线l的方程为y=mx+n（n≠0）．

由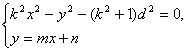

得.

由直线l与曲线C有两个不同交点，可知k²－m²≠0且

△=>0.

设M₁，M₂的坐标分别为(x₁, y₁)，(x₂, y₂)，

则，.

设M₃，M₄的坐标分别为(x₃, y₃)，(x₄，y₄)，

由得,

从而，

所以y₃+y₄=m(x₃+x₄)+2n＝m(x₁+x₂)+2n＝y₁+y₂,

所以

    于是△OM₁M₂的重心与△OM₃M₄的重心也重合．