
【题目】已知函数f(x)=2sinωx,其中常数ω>0.
(Ⅰ)令ω=1,求函数 ![]() 在
在 ![]() 上的最大值;
上的最大值;
(Ⅱ)若函数 ![]() 的周期为π,求函数g(x)的单调递增区间,并直接写出g(x)在
的周期为π,求函数g(x)的单调递增区间,并直接写出g(x)在 ![]() 的零点个数.
的零点个数.
【答案】解:(Ⅰ)函数f(x)=2sinωx,ω=1时,则f(x)=2sinx,那么:函数  =2sinx+4cos2x=4﹣4sin2x+2sinx,
=2sinx+4cos2x=4﹣4sin2x+2sinx,
令t=sinx,
∵x在 ![]() 上,
上,
∴﹣1≤t≤0
则函数F(x)转化为h(t)=﹣4t2+2t+4,
对称轴t= ![]() ,
,
∵﹣1≤t≤0,
∴h(t)的最大值为h(0)max=4,即ω=1,求函数  在
在 ![]() 上的最大值为4.
上的最大值为4.
(Ⅱ) ![]() =2﹣2sinωx+
=2﹣2sinωx+ ![]() cosωx,
cosωx,
∵周期为π,即T= ![]() ,
,
解得:ω=2
∴函数g(x)=2﹣2sin2x+ ![]() cos2x=2﹣4sin(2x﹣
cos2x=2﹣4sin(2x﹣ ![]() )=4sin(2x+
)=4sin(2x+ ![]() )+2.
)+2.
∵2x+ ![]() )∈[2k
)∈[2k ![]() ,
, ![]() ]是单调递增区间,即2k
]是单调递增区间,即2k ![]() ≤2x+
≤2x+ ![]() ≤
≤ ![]()
解得: ![]() ≤x≤
≤x≤ ![]()
函数g(x)的单调递增区间位[ ![]() ,
, ![]() ],k∈Z.
],k∈Z.
令g(x)=0,即4sin(2x+ ![]() )+2=0,
)+2=0,
解得:2x+ ![]() =2kπ﹣
=2kπ﹣ ![]() 或者2x+
或者2x+ ![]() =2kπ﹣
=2kπ﹣ ![]() ,k∈Z.
,k∈Z.
∵x在 ![]() 上.
上.
当k取2,3…6时,2x+ ![]() =2kπ﹣
=2kπ﹣ ![]() 满足要求.
满足要求.
当k取2,3…6时,2x+ ![]() =2kπ﹣
=2kπ﹣ ![]() 满足要求.
满足要求.
故得g(x)在 ![]() 上有10零点个数
上有10零点个数
【解析】(Ⅰ)根据函数f(x)=2sinωx,ω=1,化简F(x)转化为二次函数求解.(Ⅱ)利用辅助角公式化简成为y=Asin(ωx+φ)的形式,函数 ![]() 的周期为π,再利用周期公式求ω,将内层函数看作整体,放到正弦函数的增区间上,解不等式得函数的单调递增区间;(2)x∈
的周期为π,再利用周期公式求ω,将内层函数看作整体,放到正弦函数的增区间上,解不等式得函数的单调递增区间;(2)x∈ ![]() 时,求出内层函数的取值范围,结合三角函数的图象和性质,可得零点个数.
时,求出内层函数的取值范围,结合三角函数的图象和性质,可得零点个数.


 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案科目:高中数学 来源: 题型:
【题目】如图,PA⊥圆O所在的平面,AB是圆O的直径,C是圆O上的一点,E、F分别是点A在PB、PC上的射影,给出下列结论: ①AF⊥PB;②EF⊥PB;③AF⊥BC;④AE⊥平面PBC;⑤平面PBC⊥平面PAC.其中正确命题的序号是 . 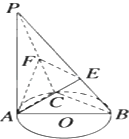
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设等差数列{an}的前n项和为Sn , 且Sn= ![]() nan+an﹣c(c是常数,n∈N*),a2=6.
nan+an﹣c(c是常数,n∈N*),a2=6.
(Ⅰ)求c的值及数列{an}的通项公式;
(Ⅱ)设bn= ![]() ,数列{bn}的前n项和为Tn , 若2Tn>m﹣2对n∈N*恒成立,求最大正整数m的值.
,数列{bn}的前n项和为Tn , 若2Tn>m﹣2对n∈N*恒成立,求最大正整数m的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义:f1(x)=f(x),当n≥2且x∈N*时,fn(x)=f(fn﹣1(x)),对于函数f(x)定义域内的x0 , 若正在正整数n是使得fn(x0)=x0成立的最小正整数,则称n是点x0的最小正周期,x0称为f(x)的n~周期点,已知定义在[0,1]上的函数f(x)的图象如图,对于函数f(x),下列说法正确的是(写出所有正确命题的编号)
①1是f(x)的一个3~周期点;
②3是点 ![]() 的最小正周期;
的最小正周期;
③对于任意正整数n,都有fn( ![]() )=
)= ![]() ;
;
④若x0∈( ![]() ,1],则x0是f(x)的一个2~周期点.
,1],则x0是f(x)的一个2~周期点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=cos(2x+φ),|φ|≤ ![]() ,若f(
,若f( ![]() ﹣x)=﹣f(x),则要得到y=sin2x的图象只需将y=f(x)的图象( )
﹣x)=﹣f(x),则要得到y=sin2x的图象只需将y=f(x)的图象( )
A.向左平移 ![]() 个单位
个单位
B.向右平移 ![]() 个单位
个单位
C.向左平移 ![]() 个单位
个单位
D.向右平移 ![]() 个单位
个单位
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax+x2﹣xlna﹣b(b∈R,a>0且a≠1),e是自然对数的底数.
(1)讨论函数f(x)在(0,+∞)上的单调性;
(2)当a>1时,若存在x1 , x2∈[﹣1,1],使得|f(x1)﹣f(x2)|≥e﹣1,求实数a的取值范围.(参考公式:(ax)′=axlna)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com