
对于三次函数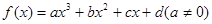 ,定义
,定义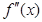 是
是 的导函数
的导函数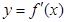 的导函数,若方程
的导函数,若方程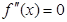 有实数解
有实数解 ,则称点
,则称点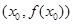 为函数
为函数 的“拐点”,可以证明,任何三次函数都有“拐点”,任何三次函数都有对称中心,且“拐点”就是对称中心,请你根据这一结论判断下列命题:
的“拐点”,可以证明,任何三次函数都有“拐点”,任何三次函数都有对称中心,且“拐点”就是对称中心,请你根据这一结论判断下列命题:
①任意三次函数都关于点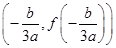 对称:
对称:
②存在三次函数 有实数解
有实数解 ,点
,点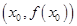 为函数
为函数 的对称中心;
的对称中心;
③存在三次函数有两个及两个以上的对称中心;
④若函数 ,则,
,则,
其中正确命题的序号为 (把所有正确命题的序号都填上).
①②④
解析试题分析:∵f(x)=ax3+bx2+cx+d(a≠0),∴f′(x)=3ax2+2bx+c,f''(x)=6ax+2b,
∵f″(x)=6a×(-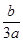 )+2b=0,∴任意三次函数都关于点(-
)+2b=0,∴任意三次函数都关于点(-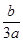 ,f(-
,f(-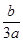 ))对称,即①正确;
))对称,即①正确;
∵任何三次函数都有对称中心,且“拐点”就是对称中心,
∴存在三次函数f′(x)=0有实数解x0,点(x0,f(x0))为y=f(x)的对称中心,即②正确;
任何三次函数都有且只有一个对称中心,故③不正确;
∵ ,∴g′(x)=x2-x,g''(x)=2x-1,
,∴g′(x)=x2-x,g''(x)=2x-1,
令g''(x)=2x-1=0,得x=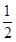 ,∵g(
,∵g(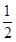 )=
)= 3-
3-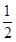 ×(
×(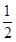 )2-
)2-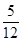 =-
=-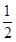 ,
,
∴函数 的对称中心是(
的对称中心是(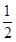 ,-
,-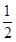 ),
),
∴g(x)+(g(1-x)=-1,
∴ ,故④正确.
,故④正确.
故答案为:①②④.
考点:应用导数研究函数的性质
点评:中档题,本题综合性较强,研究函数的图象和性质。利用导数研究函数的单调性,是常用方法。


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com