科目：高中数学 来源： 题型：解答题
（本小题满分12分）
某商店预备在一个月内分批购入每张价值为20元的书桌共36台，每批都购入x台（x是正整数），且每批均需付运费4元，储存购入的书桌一个月所付的保管费与每批购入书桌的总价值（不含运费）成正比，若每批购入4台，则该月需用去运费和保管费共52元，现在全月只有48元资金可以用于支付运费和保管费．
（1）求该月需用去的运费和保管费的总费用
（2）能否恰当地安排每批进货的数量，使资金够用？写出你的结论，并说明理由．
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
已知α，β是方程4x2－4tx－1＝0(t∈R)的两个实数根，函数f(x)＝的定义域为[α，β]．
(1)判断f(x)在[α，β]上的单调性，并证明你的结论；
(2)设g(t)＝maxf(x)－minf(x)，求函数g(t)的最小值
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
已知函数f(x)＝()x，
函数y＝f－1(x)是函数y＝f(x)的反函数．
(1)若函数y＝f－1(mx2＋mx＋1)的定义域为R，求实数m的取值范围；
(2)当x∈[－1,1]时，求函数y＝[f(x)]2－2af(x)＋3的最小值g(a)；
(3)是否存在实数m＞n＞3，使得g(x)的定义域为[n，m]，值域为[n2，m2]？若存在，求出m、n的值；若不存在，请说明理由
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
（本题满分16分）
已知函数
（
∈R且
），
.
（Ⅰ）若
，且函数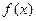
的值域为[0, ＋
)，求
的解析式；
（Ⅱ）在（Ⅰ）的条件下，当x∈[－2 , 2 ]时，
是单调函数，求实数k的取值范围；
（Ⅲ）设
，
, 且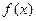是偶函数，判断
能否大于零？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
在
上为增函数．
是
，则
．
，
，
，
，即
．故函数
的极值；
若函数
在
上恰有两个不同零点，求实数 
的取值范围.
（
，且
）
的定义域；（2）判断
上是增函数，在[0，2]上是减函数，且方程
有三个根，它们分别为
．
；
的取值范围．