练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

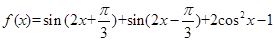    已知函数,.

    求函数的最小正周期;

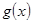    若函数的图像和的图像关于直线对称，求在上的最大值和最小值.

     

    【答案】

    （1）.(2)的最大值和最小值分别为和。

    【解析】

    试题分析：（1）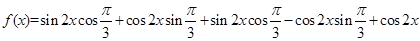 

     

    所以,的最小正周期.

    (2)    

    因为的图像和的图像关于直线对称，且关于直线对称的区间为，则在上的最大值和最小值即在的最大值和最小值。

    ∵,∴,

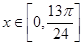    ∴当；当

    。即的最大值和最小值分别为和。

    另法：因为的图像和的图像关于直线对称，故

    ∵,∴,

    当

    当时。

    考点：和差倍半的三角函数公式，正弦型函数图象的变换，三角函数的图像和性质。

    点评：典型题，本题综合性较强，利用三角公式，将研究对象“化一”，是高考要求的基本问题，在此基础上，进一步研究函数的图象和性质。（II）小题求指定范围内函数的最值，易于出错，应结合图象分析。

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    例4、已知函数y=f（x）是定义在R上的周期函数，周期T=5，函数y=f（x）（-1≤x≤1）是奇函数．又知y=f（x）在[0，1]上是一次函数，在[1，4]上是二次函数，且在x=2时函数取得最小值-5．
    ①证明：f（1）+f（4）=0；②求y=f（x），x∈[1，4]的解析式；③求y=f（x）在[4，9]上的解析式．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知函数f（x）=2sinx+1．
    （1）设常数ω＞0，若y=f（ωx），在区间[-
    π
    2
    ，
    2π
    3
    ]上是增函数，求ω的取值范围；
    （2）当x∈[-
    π
    6
    ，
    7π
    3
    ]时，g（x）=f（x）+m恰有两个零点，求m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源：2008-2009学年四川省成都七中高三数学专项训练：从集合到函数周期（解析版） 题型：解答题

    例4、已知函数y=f（x）是定义在R上的周期函数，周期T=5，函数y=f（x）（-1≤x≤1）是奇函数．又知y=f（x）在[0，1]上是一次函数，在[1，4]上是二次函数，且在x=2时函数取得最小值-5．
    ①证明：f（1）+f（4）=0；②求y=f（x），x∈[1，4]的解析式；③求y=f（x）在[4，9]上的解析式．

    查看答案和解析>>

    科目：高中数学 来源：高考数学一轮复习必备（第09课时）：第二章 函数-函数的解析式及定义域（解析版） 题型：解答题

    例4、已知函数y=f（x）是定义在R上的周期函数，周期T=5，函数y=f（x）（-1≤x≤1）是奇函数．又知y=f（x）在[0，1]上是一次函数，在[1，4]上是二次函数，且在x=2时函数取得最小值-5．
    ①证明：f（1）+f（4）=0；②求y=f（x），x∈[1，4]的解析式；③求y=f（x）在[4，9]上的解析式．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    已知函数数学公式，其图象过点（数学公式，数学公式）．
    （1）求φ的值及y=f（x）最小正周期；
    （2）将函数y=f（x）的图象上各点的横坐标缩短到原来的数学公式，纵坐标不变，得到函数y=g（x）的图象，求函数PF2在[0，数学公式]上的最大值和最小值．

    查看答案和解析>>

    同步练习册答案