练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    已知不等式|x+2|+|x|≤a的解集不是空集，则实数a的取值范围是（ ）
    A．a＜2
    B．a≤2
    C．a＞2
    D．a≥2
    【答案】分析：通过分类讨论得到f（x）=|x+2|+|x|，则f（x）=，利用一次函数的单调性可知：f（x）≥2，要使不等式|x+2|+|x|≤a的解集不是空集，则a≥f（x）min．
    解答：解：分别令x+2=0，x=0，解得x=-2，x=0．令f（x）=|x+2|+|x|，则f（x）=，
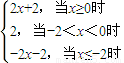
    利用一次函数的单调性可知：f（x）≥2，要使不等式|x+2|+|x|≤a的解集不是空集，则a≥2．
    故选D．
    点评：熟练掌握绝对值不等式的解法、分类讨论的思想方法、一次函数的单调性、等价转化思想等是解题的关键．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    8、已知不等式|x+2|+|x-3|≤a的解集不是空集，则实数a的取值范围是（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知不等式|x-2|＜a（a＞0）的解集为{x∈R|-1＜x＜c}，求a+2c的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2013•滨州一模）已知不等式|x+2|+|x|≤a的解集不是空集，则实数a的取值范围是（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2013•潮州二模）已知不等式|x-2|＞1的解集与不等式x2+ax+b＞0的解集相等，则a+b的值为
    -1
    -1
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知不等式|x+2|-|x-3|＞m，分别求满足下列条件m的范围：
    （1）若不等式有解；
    （2）若不等式解集为R；
    （3）若不等式解集为∅．

    查看答案和解析>>

    同步练习册答案