三角形三个顶点是A(4,0),B(6,7),C(0,3).
(1)求BC边上的中线所在的直线的方程;
(2)求BC边上的高所在的直线的方程.
【答案】
分析:(1)有中点公式求出D点坐标,由斜率率公式求出AD所在直线的斜率,点斜式求得BC边上的中线所在的直线的方程.
(2)根据垂直关系求出BC边上的高所在直线斜率,点斜式求得BC边上的高所在的直线的方程.
解答:解:(1)设BC中点为D,则D点坐标为(
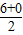
,
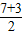
),即(3,5),∴k
AD=
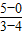
=-5,
∴AD所在直线方程为 y-0=-5(x-4),即5x+y-20=0,∴BC边上的中线所在的直线的方程为5x+y-20=0.
(2)由题意知:

,设BC边上的高所在直线斜率为k,
则k•k
BC=-1,所以,

,∴BC边上的高所在的直线的方程为
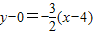
,
即3x+2y-12=0.
点评:本题考查用点斜式求直线方程的方法,其中,求直线的斜率是解题的关键.

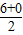 ,
,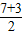 ),即(3,5),∴kAD=
),即(3,5),∴kAD=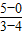 =-5,
=-5, ,设BC边上的高所在直线斜率为k,
,设BC边上的高所在直线斜率为k, ,∴BC边上的高所在的直线的方程为
,∴BC边上的高所在的直线的方程为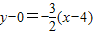 ,
,
