
 m,通过铁丝BC,CA1,CA2,CA3(A1,A2,A3是圆上三等分点且BC长度大于0)悬挂在B处,圆环呈水平状态并距天花板2m,如图所示。
m,通过铁丝BC,CA1,CA2,CA3(A1,A2,A3是圆上三等分点且BC长度大于0)悬挂在B处,圆环呈水平状态并距天花板2m,如图所示。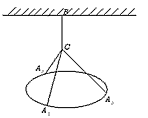
 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:高中数学 来源: 题型:
(本小题满分16分)如图所示:一吊灯的下圆环直径为4m,圆心为O,通过细绳悬挂在天花板上,圆环呈水平状态,并且与天花板的距离![]() 为2m,在圆环上设置三个等分点A1,A2,A3.点C为
为2m,在圆环上设置三个等分点A1,A2,A3.点C为![]() 上一点(不包含端点O、B),同时点C与点A1,A2,A3,B均用细绳相连接,且细绳CA1,CA2,CA3的长度相等.设细绳的总长为ym.
上一点(不包含端点O、B),同时点C与点A1,A2,A3,B均用细绳相连接,且细绳CA1,CA2,CA3的长度相等.设细绳的总长为ym.
(1)①设∠CA1O = ![]() (rad),将y表示成θ的函数关系式;
(rad),将y表示成θ的函数关系式;
②设CO=x m, 将y表示成x的函数关系式;
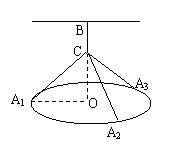 (2)请你选用(1)中的一个函数关系确定BC的长使细绳总长y 最小.
(2)请你选用(1)中的一个函数关系确定BC的长使细绳总长y 最小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com