
分析 直接利用正弦定理求出A的正弦值,利用大边对大角可求A为锐角,从而可求A的值,利用三角形内角和定理可求C的值,进而利用正弦定理可求c的值.
解答 (本题满分12分)
解:∵a=$\sqrt{2}$、b=$\sqrt{3}$、B=60°,
∴sinA=$\frac{a•sinB}{b}$=$\frac{\sqrt{2}×\frac{\sqrt{3}}{2}}{\sqrt{3}}$=$\frac{\sqrt{2}}{2}$,
∵a<b,A为锐角,
∴A=45°,C=180°-A-B=75°,
∴c=$\frac{a•sinC}{sinA}$=$\frac{\sqrt{2}×sin(30°+45°)}{\frac{\sqrt{2}}{2}}$=$\frac{\sqrt{2}+\sqrt{6}}{2}$.
点评 本题主要考查了正弦定理,大边对大角,三角形内角和定理在解三角形中的综合应用,考查计算能力和转化思想,属于基础题.


 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案科目:高中数学 来源: 题型:填空题
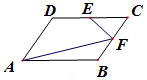 如图,菱形ABCD的边长为1,∠DAB=60°,E,F分别为DC、BC的中点,则$\overrightarrow{AF}•\overrightarrow{EF}$=$\frac{1}{8}$.
如图,菱形ABCD的边长为1,∠DAB=60°,E,F分别为DC、BC的中点,则$\overrightarrow{AF}•\overrightarrow{EF}$=$\frac{1}{8}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
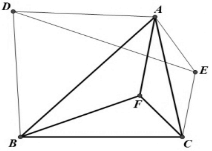 已知,△ABC内有一点F,分别以AB、AC为底边向外作等腰三角形DAB、AEC,且∠BAD=∠BCF,∠ACE=∠CBF.求证:DE平分AF.
已知,△ABC内有一点F,分别以AB、AC为底边向外作等腰三角形DAB、AEC,且∠BAD=∠BCF,∠ACE=∠CBF.求证:DE平分AF.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y+3=-2(x-1) | B. | y-3=2(x-1) | C. | y+3=4(x-1) | D. | y-3=4(x+1) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com