
(2005
福建,20)如下图,直二面角D—AB—E中,四边形ABCD是边长为2的正方形,AE=EB,F为CE上的点,且BF⊥平面ACE.(1)
求证AE⊥平面BCE;(2)
求二面角B—AC—E的大小;(3)
求点D到平面ACE的距离.
|
解析 (1)∵BF⊥平面ACE,∴BF⊥AE.∵二面角D—AB—E为直二面角,且CB⊥AB,∴CB⊥平面ABE,∴CB⊥AE,∴AE⊥平面BCE.(2) 以线段AB的中点为原点O,OE所在直线为x轴,AB所在直线为y轴,过O点平行于AD的直线为z轴,建立空间直角坐标系O-xyz,如下图.因为AE⊥面BCE,BE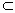 面BCE,所以AE⊥BE,在Rt△AEB中,AB=2,O为AB的中点,故OE=1.于是A(0,-l,0),E(1,0,0),C(0,1,2). 面BCE,所以AE⊥BE,在Rt△AEB中,AB=2,O为AB的中点,故OE=1.于是A(0,-l,0),E(1,0,0),C(0,1,2).
 .设平面AEC的一个法向量为n=(x,y,z),则 .设平面AEC的一个法向量为n=(x,y,z),则 即 即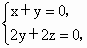
解得  令y=-1,得n=(1,-1,1)是平面AEC的一个法向量.又平面BAC的一个法向量为m=(1,0,0), 令y=-1,得n=(1,-1,1)是平面AEC的一个法向量.又平面BAC的一个法向量为m=(1,0,0),
故 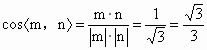 . .
∴二面角 B—AC—E的大小为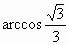 . .
(3) ∵AD∥z轴,AD=2,故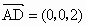 . .
∴点 D到平面ACE的距离
|
|
剖析: 1.在平面BCE内寻找两条相交直线都与AE垂直,结合题设可知,BF和BC即是.2 .找二面角B—AC—E的平面角.∵ BF⊥平面AEC,只需作BG⊥AC于G,连FG即可;而ABCD为正方形,所以G为AC和BD的交点.3 .用体积法较方便. |


 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com