

(1)求证:AB2=AG·BF;
(2)证明EG与⊙O相切,并求AG、BF的长.
思路解析:由正五边形的特征,易得到△EAG∽△FBC;连结EF,易证EF⊥EG,再用切割线定理完成计算.
证明:(1)易证五边形ABCDE的外角∠FCB=∠EAG=∠FBC,
∵EG∥CB,∴∠G=∠FBC.
∴△EAG∽△FBC.
∴![]() ,即BC·AE=AG·BF.
,即BC·AE=AG·BF.
又∵BC=AE=AB,
∴AB2=AG·BF. ①
(2)连结EF,由(1)可知FB=FC,即△FBC为等腰三角形,易知BA=CD,
∴FA=FD.

∴EF⊥BC且EF平分BC.
∴EF过圆心O.
又∵EG∥CB,∴EF⊥EG.
∴EG与⊙O相切.
∴EG2=AG·BG.
由(1)可知∠G=∠EAG,
∴EG=EA=2.
设AG=x,则22=x(x+2).解得x=![]() -1.
-1.
∴AG=![]() -1.代入①中可得BF=
-1.代入①中可得BF=![]() +1.
+1.


科目:高中数学 来源: 题型:
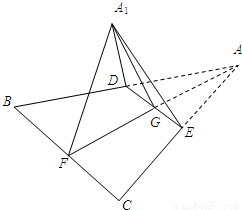
 (2008•成都二模)如图,已知边长为2的正三角形ABC中线AF与中位线DE相交于点G,将此三角形沿DE折成二面角A1-DE-B,设二面角A1-DE-B的大小为θ,则当异面直线A1E与BD的夹角为60°时,cosθ的值为( )
(2008•成都二模)如图,已知边长为2的正三角形ABC中线AF与中位线DE相交于点G,将此三角形沿DE折成二面角A1-DE-B,设二面角A1-DE-B的大小为θ,则当异面直线A1E与BD的夹角为60°时,cosθ的值为( )查看答案和解析>>
科目:高中数学 来源:2010-2011学年四川省成都市双流中学高三(下)2月月考数学试卷(文科)(解析版) 题型:选择题




查看答案和解析>>
科目:高中数学 来源:2008年四川省成都市高考数学二模试卷(理科)(解析版) 题型:选择题





查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com