Question

已知实数a，b，c满足a+2b-c=1，则a²+b²+c²的最小值是________．

Answer 1

分析：利用条件a+2b-c=1，构造柯西不等式（a+2b-c）²≤（1²+2²+1²）（a²+b²+c²）进行解题即可．
解答：由柯西不等式得（a+2b-c）²≤（1²+2²+1²）（a²+b²+c²），
∵a+2b-c=1，
∴1≤（1²+2²+1²）（a²+b²+c²），
∴，
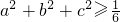
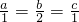
当且仅当 取等号，
则a²+b²+c²的最小值是
故答案为：．
点评：本题主要考查了函数的值域，以及柯西不等式的应用，解题的关键是利用（a+2b-c）²≤（1²+2²+1²）（a²+b²+c²），进行解题，属于中档题．