
从一副混合后的扑克牌( 52张)中随机抽取1张,事件A为“抽得为红桃K”,事件B为“抽得为黑桃”,则概率P(A∪B)=________.(结果用最简分数表示)
52张)中随机抽取1张,事件A为“抽得为红桃K”,事件B为“抽得为黑桃”,则概率P(A∪B)=________.(结果用最简分数表示)
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案科目:高中数学 来源: 题型:
经销商经销某种农产品,在一个销售季度内,每售出1 t该产品获利润500元,未售出的产品,每1 t亏损300元.根据历史资料,得到销售季度内市场需求量的频率分布直方图,如图所示.经销商为下一个销售季度购进了130 t该农产品.以X(单位:t,100≤X≤150)表示下一个销售季度内的市场需求量,T(单位:元)表示下一个销售季度内经销该农产品的利润.
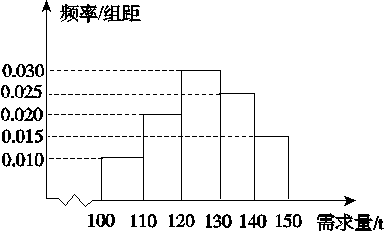
(1)将T表示为X的函数;
( 2)根据直方图估计利润T不少于57 000元的概率.
2)根据直方图估计利润T不少于57 000元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
一个容量为100的样本,其数据的分组与各组的频数如下表
| 组别 | (0,10] | (10,20] | (20,30] | (30,40] | (40,50] | (50,60] | (60,70] |
| 频数 | 12 | 13 | 24 | 15 | 16 | 13 | 7 |
则样本数据落在(10,40]上的频率为( )
A.0.13 B.0.39
C.0. 52 D.0.64
52 D.0.64
查看答案和解析>>
科目:高中数学 来源: 题型:
从某居民区随机抽取10个家庭,获得第i个家庭的月收入xi(单位:千元)与月储蓄yi(单位:千元)的数据资料,算得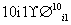 xi=80,
xi=80,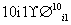 yi=20,
yi=20,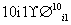 xiyi=184,
xiyi=184,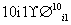 x
x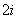 =720.
=720.
(1)求家庭的月储蓄y对月收入x的线性回归方程y=bx+a;
(2)判断变量x与y之间是正相关还是负相关;
(3)若该居民区某家庭月收入为7千元,预测该家庭的月储蓄.
附:线性回归方程y=bx+a中,b=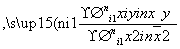 ,a=
,a=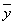 -
- b
b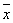 ,
,
其中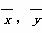 为样本平均值.线性回归方程也可写为
为样本平均值.线性回归方程也可写为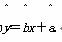
查看答案和解析>>
科目:高中数学 来源: 题型:
小莉与小明一起用A,B两枚均匀的小立方体(立方体的每个面上分别标有数字1,2,3,4,5,6)玩游戏,以小莉掷的A立方体朝上的数字为x,小明掷的B立方体朝上的数字为y,来确定点P(x,y),那么他们各掷一次所确定的点P(x,y)落在已知抛物线y=-x2+4x上的概率为( )
A. B.
B.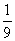
C.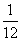 D.
D.
查看答案和解析>>
科目:高中数学 来源: 题型:
投掷一个质地均匀、每个面上标有一个数字的正方体玩具,它的六个面中,有两个面的数字是0,两个面的数字是2,两个面的数字是4.将此玩具连续抛掷两次,以两次朝上一面出现的数字分别作为点P的横坐标和纵坐标.
(1)求点P落在区域C:x2+y2≤10上的概率;
(2)若以落在区域C上的所有点为顶点作面积最大的多边形区域M,在区域C上随机撒一粒豆子,求豆子落在区域M上的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
执行如图所示的程序框图,若输出的结果是9,则判断框内m的取值范围是( )
A.(42,56] B.(56,72]
C.(72 ,90] D.(42,90]
,90] D.(42,90]
查看答案和解析>>
科目:高中数学 来源: 题型:
已知中心在坐标原点,以坐标轴为对称轴的双曲线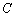 过点
过点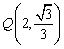 ,且
,且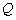 点在
点在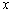 轴上的射影恰为该双曲线的焦点
轴上的射影恰为该双曲线的焦点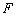 .
.
(Ⅰ)求双曲线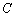 的方程;
的方程;
(Ⅱ)过双曲线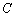 的焦点
的焦点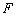 作与
作与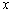 轴不垂直的任意直线
轴不垂直的任意直线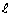 交双曲线
交双曲线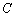 于
于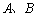 两点,线段
两点,线段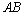 的垂直平分线交
的垂直平分线交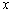 轴于点
轴于点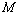 ,问:
,问: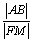 是否为定值?若为定值,请求出这个定值;若不是定值,请说明理由.
是否为定值?若为定值,请求出这个定值;若不是定值,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com