
【题目】如图放置的边长为1的正方形![]() 沿
沿![]() 轴滚动,点
轴滚动,点![]() 恰好经过原点.设顶点
恰好经过原点.设顶点![]() 的轨迹方程是
的轨迹方程是![]() ,则对函数
,则对函数![]() 有下列判断:①函数
有下列判断:①函数![]() 是偶函数;②对任意的
是偶函数;②对任意的![]() ,都有
,都有![]() ;③函数
;③函数![]() 在区间
在区间![]() 上单调递减;④函数
上单调递减;④函数![]() 的值域是
的值域是![]() ;⑤
;⑤![]() .其中判断正确的序号是__________.
.其中判断正确的序号是__________.

【答案】①②⑤
【解析】
根据正方形的运动,得到点P的轨迹方程,然后根据函数的图象和性质分别进行判断即可.
当﹣2≤x≤﹣1,P的轨迹是以A为圆心,半径为1的![]() 圆,
圆,
当﹣1≤x≤1时,P的轨迹是以B为圆心,半径为![]() 的
的![]() 圆,
圆,
当1≤x≤2时,P的轨迹是以C为圆心,半径为1的![]() 圆,
圆,
当3≤x≤4时,P的轨迹是以A为圆心,半径为1的![]() 圆,
圆,
∴函数的周期是4.
因此最终构成图象如下:
①,根据图象的对称性可知函数y=f(x)是偶函数,故①正确;
②,由图象即分析可知函数的周期是4.
即f(x+4)=f(x),即f(x+2)=f(x﹣2),故②正确;
③,函数y=f(x)在区间[2,3]上单调递增,
故③错误;
④,由图象可得f(x)的值域为[0,![]() ],故④错误;
],故④错误;
⑤,根据积分的几何意义可知![]() f(x)dx
f(x)dx![]() π(
π(![]() )2
)2![]() 1×1
1×1![]() π×12
π×12![]() ,
,
故⑤正确.
故答案为:①②⑤.


科目:高中数学 来源: 题型:
【题目】为推动文明城市创建,提升城市整体形象,2018年12月30日盐城市人民政府出台了《盐城市停车管理办法》,2019年3月1日起施行.这项工作有利于市民养成良好的停车习惯,帮助他们树立绿色出行的意识,受到了广大市民的一致好评.现从某单位随机抽取80名职工,统计了他们一周内路边停车的时间![]() (单位:小时),整理得到数据分组及频率分布直方图如下:
(单位:小时),整理得到数据分组及频率分布直方图如下:

组号 | 分组 | 频数 |
1 |
| 6 |
2 |
| 8 |
3 |
| 22 |
4 |
| 28 |
5 |
| 12 |
6 |
| 4 |
(1)从该单位随机选取一名职工,试计算这名职工一周内路边停车的时间少于8小时的频率;
(2)求频率分布直方图中![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的两个焦点
的两个焦点![]() ,
,![]() ,且椭圆过点
,且椭圆过点![]() ,
,![]() ,且
,且![]() 是椭圆上位于第一象限的点,且
是椭圆上位于第一象限的点,且![]() 的面积
的面积![]() .
.
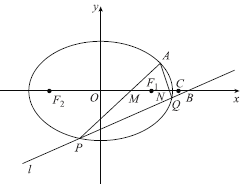
(1)求点![]() 的坐标;
的坐标;
(2)过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相交于点
相交于点![]() ,
,![]() ,直线
,直线![]() ,
,![]() 与
与![]() 轴相交于
轴相交于![]() ,
,![]() 两点,点
两点,点![]() ,则
,则![]() 是否为定值,如果是定值,求出这个定值,如果不是请说明理由.
是否为定值,如果是定值,求出这个定值,如果不是请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,n∈N*.
,n∈N*.
(1)设f(x)=a0+a1x+a2x2+…+anxn,
①求a0+a1+a2+…+an;
②若在a0,a1,a2,…,an中,唯一的最大的数是a4,试求n的值;
(2)设f(x)=b0+b1(x+1)+b2(x+1)2+…+bn(x+1)n,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2012年12月18日,作为全国首批开展空气质量新标准监测的74个城市之一,郑州市正式发布![]() 数据.资料表明,近几年来,郑州市雾霾治理取得了很大成效,空气质量与前几年相比得到了很大改善.郑州市设有9个监测站点监测空气质量指数(
数据.资料表明,近几年来,郑州市雾霾治理取得了很大成效,空气质量与前几年相比得到了很大改善.郑州市设有9个监测站点监测空气质量指数(![]() ),其中在轻度污染区、中度污染区、重度污染区分别设有2,5,2个监测站点,以9个站点测得的
),其中在轻度污染区、中度污染区、重度污染区分别设有2,5,2个监测站点,以9个站点测得的![]() 的平均值为依据,播报我市的空气质量.
的平均值为依据,播报我市的空气质量.
(Ⅰ)若某日播报的![]() 为118,已知轻度污染区
为118,已知轻度污染区![]() 的平均值为74,中度污染区
的平均值为74,中度污染区![]() 的平均值为114,求重度污染区
的平均值为114,求重度污染区![]() 的平均值;
的平均值;
(Ⅱ)如图是2018年11月的30天中![]() 的分布,11月份仅有一天
的分布,11月份仅有一天![]() 在
在![]() 内.
内.
组数 | 分组 | 天数 |
第一组 |
| 3 |
第二组 |
| 4 |
第三组 |
| 4 |
第四组 |
| 6 |
第五组 |
| 5 |
第六组 |
| 4 |
第七组 |
| 3 |
第八组 |
| 1 |
①郑州市某中学利用每周日的时间进行社会实践活动,以公布的![]() 为标准,如果
为标准,如果![]() 小于180,则去进行社会实践活动.以统计数据中的频率为概率,求该校周日进行社会实践活动的概率;
小于180,则去进行社会实践活动.以统计数据中的频率为概率,求该校周日进行社会实践活动的概率;
②在“创建文明城市”活动中,验收小组把郑州市的空气质量作为一个评价指标,从当月的空气质量监测数据中抽取3天的数据进行评价,设抽取到![]() 不小于180的天数为
不小于180的天数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() ,点
,点![]() 在椭圆
在椭圆![]() 上,椭圆
上,椭圆![]() 的离心率是
的离心率是![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设点![]() 为椭圆长轴的左端点,
为椭圆长轴的左端点,![]() 为椭圆上异于椭圆
为椭圆上异于椭圆![]() 长轴端点的两点,记直线
长轴端点的两点,记直线![]() 斜率分别为
斜率分别为![]() ,若
,若![]() ,请判断直线
,请判断直线![]() 是否过定点?若过定点,求该定点坐标,若不过定点,请说明理由.
是否过定点?若过定点,求该定点坐标,若不过定点,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1所示,在![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 为
为![]() 的平分线,点
的平分线,点![]() 在线段
在线段![]() 上,
上, ![]() .如图2所示,将
.如图2所示,将![]() 沿
沿![]() 折起,使得平面
折起,使得平面![]() 平面
平面![]() ,连结
,连结![]() ,设点
,设点![]() 是
是![]() 的中点.
的中点.
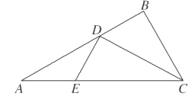

图1 图2
(1)求证: ![]() 平面
平面![]() ;
;
(2)在图2中,若![]() 平面
平面![]() ,其中
,其中![]() 为直线
为直线![]() 与平面
与平面![]() 的交点,求三棱锥
的交点,求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com