
(本小题12分)如图,四棱锥 中,
中,
侧面 是边长为2的正三角形,且与底面垂直,底面
是边长为2的正三角形,且与底面垂直,底面 是
是 的菱形,
的菱形, 为
为 的中点.
的中点.
(1)求 与底面
与底面 所成角的大小;
所成角的大小;
(2)求证: 平面
平面 ;
;
(3)求二面角 的余弦值.
的余弦值.

(1)取DC的中点O,由ΔPDC是正三角形,有PO⊥DC.
又∵平面PDC⊥底面ABCD,∴PO⊥平面ABCD于O.
连结OA,则OA是PA在底面上的射影.∴∠PAO就是PA与底面所成角.
∵∠ADC=60°,由已知ΔPCD和ΔACD是全等的正三角形,从而求得OA=OP=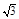 .
.
∴∠PAO=45°.∴PA与底面ABCD可成角的大小为45°.
(2)由底面ABCD为菱形且∠ADC=60°,DC=2,DO=1,有OA⊥DC.
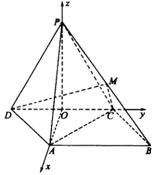 建立空间直角坐标系如图,则
建立空间直角坐标系如图,则 ,
, 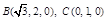 .
.
由M为PB中点,∴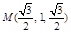 .
.
∴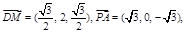
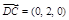 .
.
∴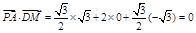 ,
,
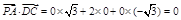 .
.
∴PA⊥DM,PA⊥DC. ∴PA⊥平面DMC.
(3)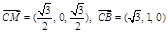 .令平面BMC的法向量
.令平面BMC的法向量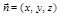 ,
,
则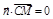 ,从而x+z=0; ……①,
,从而x+z=0; ……①, 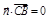 ,从而
,从而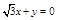 . ……②
. ……②
由①、②,取x=−1,则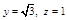 .
∴可取
.
∴可取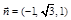 .
.
由(2)知平面CDM的法向量可取 ,
,
∴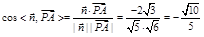 . ∴所求二面角的余弦值为-
. ∴所求二面角的余弦值为-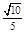 .
.
法二:(1)方法同上
(2)取 的中点
的中点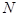 ,连接
,连接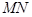 ,由(Ⅰ)知,在菱形
,由(Ⅰ)知,在菱形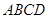 中,由于
中,由于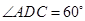 ,则
,则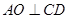 ,又
,又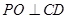 ,则
,则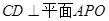 ,即
,即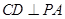 ,
,
又在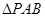 中,中位线
中,中位线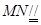
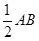 ,
,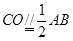 ,则
,则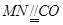 ,则四边形
,则四边形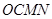 为
为 ,所以
,所以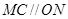 ,在
,在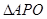 中,
中,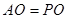 ,则
,则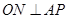 ,故
,故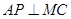 而
而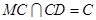 ,
,
则
(3)由(2)知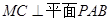 ,则
,则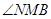 为二面角
为二面角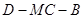 的平面角,在
的平面角,在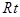
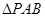 中,易得
中,易得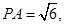
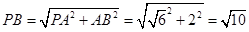 ,
,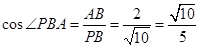 ,
,
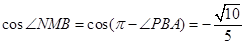 故,所求二面角的余弦值为
故,所求二面角的余弦值为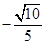
【解析】略


科目:高中数学 来源:2010-2011学年湖南省常德市高三质量检测考试数学理卷 题型:解答题
(本小题12分)
如图3,已知在侧棱垂直于底面
的三棱柱 中,AC=BC, AC⊥BC,点D是A1B1中点.
中,AC=BC, AC⊥BC,点D是A1B1中点.
(1)求证:平面AC1D⊥平面A1ABB1;
(2)若AC1与平面A1ABB1所成角的正弦值
为 ,求二面角D- AC1-A1的余弦值.
,求二面角D- AC1-A1的余弦值.

查看答案和解析>>
科目:高中数学 来源:2014届海南省高一上学期教学质量监测三数学 题型:解答题
(本小题12分)如图,四棱锥 中,底面
中,底面 是正方形,
是正方形, ,
,  底面
底面 ,
,  分别在
分别在 上,且
上,且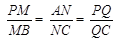
(1)求证:平面 ∥平面
∥平面 .
.
(2)求直线 与平面面
与平面面 所成角的正弦值.
所成角的正弦值.

查看答案和解析>>
科目:高中数学 来源:2010-2011年海南省高二下学期质量检测数学文卷(一) 题型:解答题
(本小题12分)
如图:⊙O为△ABC的外接圆,AB=AC,过点A的直线交⊙O于D,交BC延长线于F,DE是BD的延长线,连接CD。
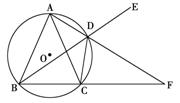
① 求证:∠EDF=∠CDF;
②求证:AB2=AF·AD。
查看答案和解析>>
科目:高中数学 来源:2009-2010集宁一中学高三年级理科数学第一学期期末考试试题 题型:解答题
(本小题12分)如图,四面体ABCD中,O、E分别是BD、BC的中点,

(I)求证: 平面BCD;
平面BCD;
(II)求异面直线AB与CD所成角的大小;
(III)求点E到平面ACD的距离。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com