
 ,则n=________.
,则n=________. ,利用古典概型的概率公式求出“没有女生”的概率,根据对立事件的概率公式得到方程求出n的值.
,利用古典概型的概率公式求出“没有女生”的概率,根据对立事件的概率公式得到方程求出n的值.
 ,
,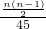 =
= ,
,

 活力课时同步练习册系列答案
活力课时同步练习册系列答案科目:高中数学 来源:2010-2011学年江西省高三第二学期第一次模拟考试文科数学 题型:解答题
(本小题满分为12分)
某中学研究性学习小组,为了考察高中学生的作文水平与爱看课外书的关系,在本校高三年级随机调查了 名学生。调査结果表明:在爱看课外书的
名学生。调査结果表明:在爱看课外书的 人中有
人中有 人作文水平好,另
人作文水平好,另 人作文水平一般;在不爱看课外书的
人作文水平一般;在不爱看课外书的 人中有
人中有 人作文水平好,另
人作文水平好,另 人作文水平一般.
人作文水平一般.
(Ⅰ)试根据以上数据建立一个 列联表,并运用独立性检验思想,指出有多大把握认为中学生的作文水平与爱看课外书有关系?
列联表,并运用独立性检验思想,指出有多大把握认为中学生的作文水平与爱看课外书有关系?
(Ⅱ)将其中某5名爱看课外书且作文水平好的学生分别编号为 ,某
,某 名爱看课外书且作文水平一般的学生也分别编号为
名爱看课外书且作文水平一般的学生也分别编号为 ,从这两组学生中各任选
,从这两组学生中各任选 人进行学习交流,求被选取的两名学生的编号之和为
人进行学习交流,求被选取的两名学生的编号之和为 的倍数或
的倍数或 的倍数的概率.
的倍数的概率.
附:
临界值表:
|
|
0. 10 |
0. 05 |
0. 025 |
0.010 |
0. 005 |
0. 001 |
|
|
2. 706 |
3. 841 |
5. 024 |
6. 635 |
7. 879 |
10. 828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题满分为12分)
某中学研究性学习小组,为了考察高中学生的作文水平与爱看课外书的关系,在本校高三年级随机调查了![]() 名学生。调査结果表明:在爱看课外书的
名学生。调査结果表明:在爱看课外书的![]() 人中有
人中有![]() 人作文水平好,另
人作文水平好,另![]() 人作文水平一般;在不爱看课外书的
人作文水平一般;在不爱看课外书的![]() 人中有
人中有![]() 人作文水平好,另
人作文水平好,另![]() 人作文水平一般.
人作文水平一般.
(Ⅰ)试根据以上数据建立一个![]() 列联表,并运用独立性检验思想,指出有多大把握认为中学生的作文水平与爱看课外书有关系?
列联表,并运用独立性检验思想,指出有多大把握认为中学生的作文水平与爱看课外书有关系?
(Ⅱ)将其中某5名爱看课外书且作文水平好的学生分别编号为![]() ,某
,某![]() 名爱看课外书且作文水平一般的学生也分别编号为
名爱看课外书且作文水平一般的学生也分别编号为![]() ,从这两组学生中各任选
,从这两组学生中各任选![]() 人进行学习交流,求被选取的两名学生的编号之和为
人进行学习交流,求被选取的两名学生的编号之和为![]() 的倍数或
的倍数或![]() 的倍数的概率.
的倍数的概率.
附:![]()
临界值表:
|
| 0. 10 | 0. 05 | 0. 025 | 0.010 | 0. 005 | 0. 001 |
|
| 2. 706 | 3. 841 | 5. 024 | 6. 635 | 7. 879 | 10. 828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com