
 设函数
设函数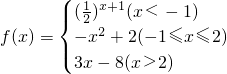 .
. 解:(Ⅰ) 函数f(x)的图象如图.…
解:(Ⅰ) 函数f(x)的图象如图.…

 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案科目:高中数学 来源: 题型:
 某厂制造A种电子装置45台,B种电子装置55台,为了给每台装置装配一个外壳,要从两种不同规格的薄钢板上截取.已知甲种薄钢板每张面积为2m2,可做A种外壳3个和B种外壳5个;乙种薄钢板每张面积为3m2,可做A种和B种外壳各6个,用这两种薄钢板各多少张,才能使总的用料面积最小?(请根据题意,在下面的横线处按要求填上恰当的关系式或数值)
某厂制造A种电子装置45台,B种电子装置55台,为了给每台装置装配一个外壳,要从两种不同规格的薄钢板上截取.已知甲种薄钢板每张面积为2m2,可做A种外壳3个和B种外壳5个;乙种薄钢板每张面积为3m2,可做A种和B种外壳各6个,用这两种薄钢板各多少张,才能使总的用料面积最小?(请根据题意,在下面的横线处按要求填上恰当的关系式或数值)
|
|
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com